一:弹性压杆的稳定的再论述
文章稳定问题(一)分析了完全弹性时受压杆稳定欧拉临界荷载问题。可以形象的想象一根橡胶杆,即使失稳后被压的杆端着地了,也不会破坏,欧拉临界力就是这样得出来的,见下图:
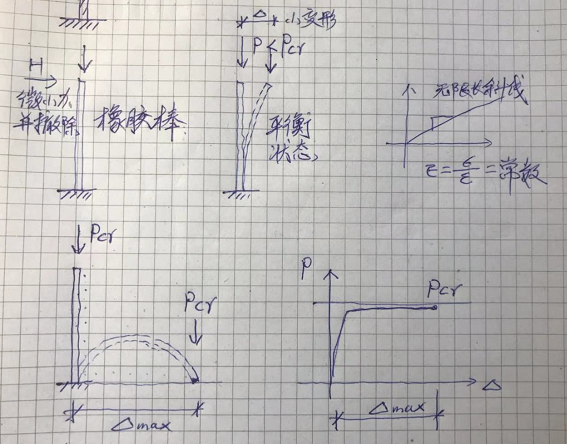
文(一)在绘制 草图时,把失稳后画成下降段了,是错误的,应为平直的。如果是完全弹性压杆,即此时的压力不能变小,否则又会弹了起来。我们实际工程中的材料总有材料的屈服问题,所以会存在上图红笔所画的那样的压力下降段,造成我对完全弹性也存在下降段的错误理解。完全弹性的杆可以理解成两个小伙子摔跤,一个摁摔倒一个后,死死摁住丝毫不敢放松,除非那个被压的人自己泄了劲就好像材料发生了塑性时一样。
弹性材料压杆的临界力和长细比和E有关,见下图:
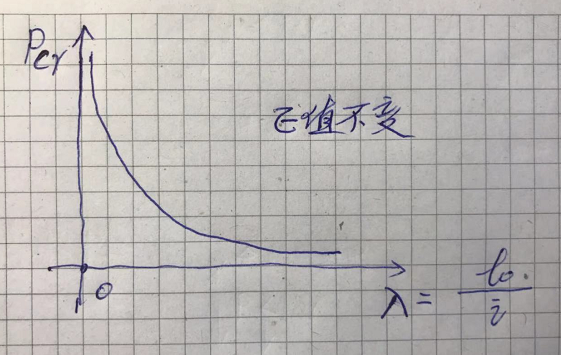
很容易理解,当长细比很小的时候,欧拉稳定应力可以无限大,就像我们压一个橡胶垫,橡胶点可以承受巨大的压力。长细比很大的时候,杆的自重就可以使其失稳,比如桌面上一张立着的薄纸的弯曲。
但砖石、木材、混凝土、钢材等建筑材料没有一种像橡胶那样的材料,所以单纯的研究欧拉临界力没有多大意义,要考虑材料本身的特性即材料的非线性来和稳定压力一块来研究才有价值。
二:材料几何非线性、材料非线性对稳定压力的影响
几乎所有的建筑材料都是非线性的,即使弹性阶段,其弹性模量也可能是非线性的,更不要说塑性阶段了,一般是弹塑性相伴而行。还有钢材的残余应力也会使断面提前进入屈服,使其的弹性模量刚度消失。所以实际的工程受压构件的稳定压力一定小于欧拉临界压力。
实际结构的稳定问题应该包括几何非线性(结构受压稳定问题(二)_6、及加工安装误差)、材料非线性(材料的应力应变曲线和残余应力等)。
一般而言,这种非线性只能采用强大的计算机数值分析方法。
过去没有计算机的年代,发展过简化的计算方法比如切线模量法和折算模量法。这些方法根本上还是利用欧拉公式,只是弹性模量E根据材料的非线性进行了折减,很粗略,无法和现在的数值分析相比。
无需进行数值分析,仅通过概念就可以大概画出考虑材料非线性时的结构受压稳定问题(二)_7曲线。
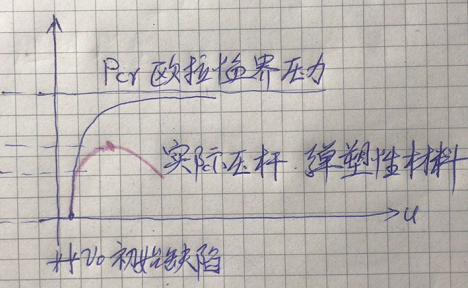
如果从研究极限承载力的角度来说,图中的红色的的曲线不能包含所有的情况。有的杆件失稳屈曲后承载力仍可提高,比如稳定分叉失稳和拱屋面的越屈失稳等。但对于实际的工程,一般都会避免任何失稳,除非考虑防倒塌的情况,所以这种复杂的失稳理论本文就略去了,实话说也是我的能力之外。
综合考虑材料的几何非线性、材料非线性、残余应力等受压杆的稳定压力变化如下图(红色曲线):
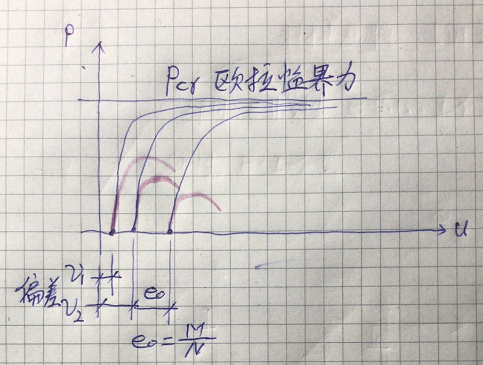
(1)几何非线性如构件加工安装偏差如上图中的结构受压稳定问题(二)_10、结构受压稳定问题(二)_11,偏差越大,稳定压力越小。
(2)计算弯矩的影响。本质上和偏差形成的初始弯矩PV是一样的,弯矩(一阶)是计算出来的,不像偏差是加工安装问题。有弯矩的压杆为压弯构件,但注意这里的压弯构件的弯曲变形仍属于小变形的范围,是符合欧拉公式的推导的小变形范畴的,而且以受压为主,建筑结构工程中的框架柱基本都属于压弯构件。假如弯矩成为主导,就不是失稳问题了,成为了垂直杆的受弯问题了,见下图的对比:

(3)材料的非线性本质是改变了杆件的弹性模量E和断面边缘出现屈服时的I,见下图:

所以非线弹性的材料的稳定压力的降低就是比较容易理解的了。
(4)值得说明下,残余应力不会改变不考虑稳定时受压短杆或受拉杆的最大承载力fA,但会减少有弯曲下的受压杆的失稳压力,是因为受弯杆件压区残余应力会提前使材料进入屈服减少了杆件的刚度E造成的。

三:长细比和受压稳定系数图片
长细比是我们结构工程师最基本的概念,再简述一下,见下图:

红色的曲线是实际受压杆最大的稳定压力的关系图。首先最大压力小于等于fA,这是不考虑失稳时的极短柱的最大的承载能力,然后在长细比的增加开始阶段,最大受压承载力缓慢减少,这是短柱时长细比对承载力影响很小。当长细比较大时,承载力下降很快,即所谓长柱时失稳压力迅速变小。
红色的曲线无法采用欧拉那样的解析解求解,过去也没有计算机,前辈们根据实验和理论分析建立了稳定系数的设计方法。
稳定系数
这个结构受压稳定问题(二)_16是综合出来的系数,一定小于欧拉临界力那样算出来的系数。
这个系数和构件的如下条件有关:长细比、材料非线性本构关系、构件缺陷、残余应力。后三者属于构件自身几何和材料层面的,而长细比的确定就比较复杂了,首先要确定计算长度。计算长度和整体结构、构件约束、所受的一阶弯矩等均有关系,比如构件的计算长度和其两端的约束有关,规范框架结构柱的计算长度表就是根据这个来的,首层因为基础是嵌固,所以相对于标准层计算长度就小。
钢结构框架相对混凝土的框架柔的多,所以很多需要采用框架-支撑结构。这种结构比纯框架的水平侧移小的多,楼层侧移的大小和柱子的计算长度关系很大,所以钢结构框架柱在确定计算长度的时候要分有侧移框架和无侧移框架。带支撑或剪力墙的是无侧移,纯框架是有侧移。当然设置的支撑太少太弱也不能叫做无侧移,规范有专门判定是否为无侧移的公式,不符合是不能按无侧移来确定计算长度的否则可能不安全。
计算长度和长细比是钢结构规范的重点内容,仅长细比和计算长度的内容钢结构设计规范就占了几十页的篇幅。
四:钢结构柱与混凝土结构柱压弯计算的不同
上文(二)介绍的基本是钢结构受压柱的受力状态,其计算公式如下图:
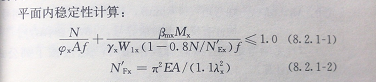
可以看做两个部分,一是轴力部分,其稳定系数包含了杆件初始偏差、长细比和材料的影响,二是弯矩部分,和柱两端的弯矩情况、材料非线性有关。
混凝土柱与钢结构考虑的方法不同,《混规》6.2.3规定当柱子的长细比满足一定条件时,可以不考虑柱挠曲长生的附加弯矩的影响。
但柱子弯矩要增加一个附加偏心距(《混规》6.2.5),按20mm和截面的h/30的大值计算,然后就可以按大、小偏心受压柱去计算了。
这是因为混凝土柱材料和几何尺寸的特点造成的,大家可以自己思考一下,挺有意思的。
五:
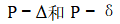
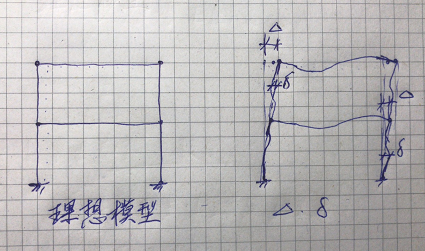
当结构受水平力有偏移时,结构楼层(构件的上下端连直线)有位移差(或位移角),这个位移叫大△,因安装偏差造成的结构偏移也叫大△。构件自身受压受弯屈曲或构件加工偏差产生的构件弯曲都叫小结构受压稳定问题(二)_19,见下图:
六:一阶分析的概念及仅一阶分析设计的前提条件
为什么叫一阶分析,因为是上述的构件截面计算外荷载效应的过程中,没有计算初始偏差、初始弯矩产生的P△和结构受压稳定问题(二)_21增加及材料非线性的效应。前辈们不是不知道有这个影响,是因为当时只有计算尺,无法算的精细,只好采用考虑长细比下的稳定系数来综合考虑了。比如轴线受压构件,我们只计算轴力N,就可以与考虑稳定的最大轴力做比较了。框架结构的框架柱,我们算出垂直力工况作用下的N 和水平力比如地震和风荷载作用工况组合作用下的M ,用这两个数据就可以计算柱子的承载力是否符合要求了,其构件的计算公式已经包含了结构受压稳定问题(二)_22、较小P△及材料非线性的不利的影响。
上文已经讲过 P△是不同的,P△是考虑构件自身弯曲和加工缺陷的那个,P△是考虑结构整体侧移和安装偏差的那个△。即使一个完全没有侧移的结构,构件自身也会有缺陷和弯矩形成的弯曲的结构受压稳定问题(二)_26。规范压弯构件的稳定系数主要考虑的是这个小结构受压稳定问题(二)_27的影响,当然也有包含较小的△的影响。新钢标规定当这个较小的P-△弯矩占总弯矩不超过10%时可以采用一阶分析进行计算。混凝土高规5.4.1条规定是刚重比小于下面的规定时才可以用一阶分析计算。

新钢标5.3.1和5.3.2 (见下图)的规定一阶分析时要用6~8章的进行构件计算,6~8章是几十年来一批又一批的前辈们总结并列入规范的传统的方法。

换句话说,如果不采用一阶分析,而是采用更加精确的二阶或直接分析,就不必完全用这些规定计算了。是什么意思呢?那如何计算呢?
新钢标规定当结构的P△超过10%的时候,混高规是不满足5.4.1的要求时,靠构件本身的综合稳定系数及混凝土构件的那个计算就不安全了,所以要计算P△的影响,叫二阶分析。二阶分析可以用有限元的方法,也可以简单一些,直接在一阶分析的M的基础上乘以一个增大系数,都属于二阶分析。还有更精确的叫直接分析,笔者会继续谈的,但不知道能不能说的清楚。
