1.等效和等效电路
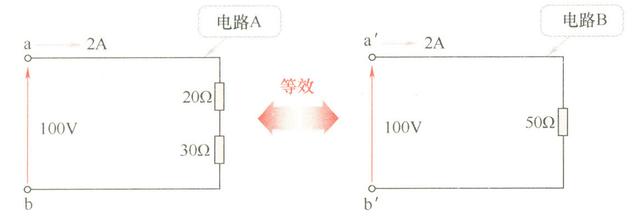
如图所示的两个电路,其两端电压都为100V,电路中的电流均为2A,所以ab间和a"b"间的电路是等效的。电路A对电路B,还有电路B对电路A互相成为等效电路。尽管互为等效的两个电路的组成不同,但只要两个电路中的电流和电压都是相等的,则称其为等效电路。
2.从△联结电路到Y联结电路的变换(△-Y变换)
[实例]
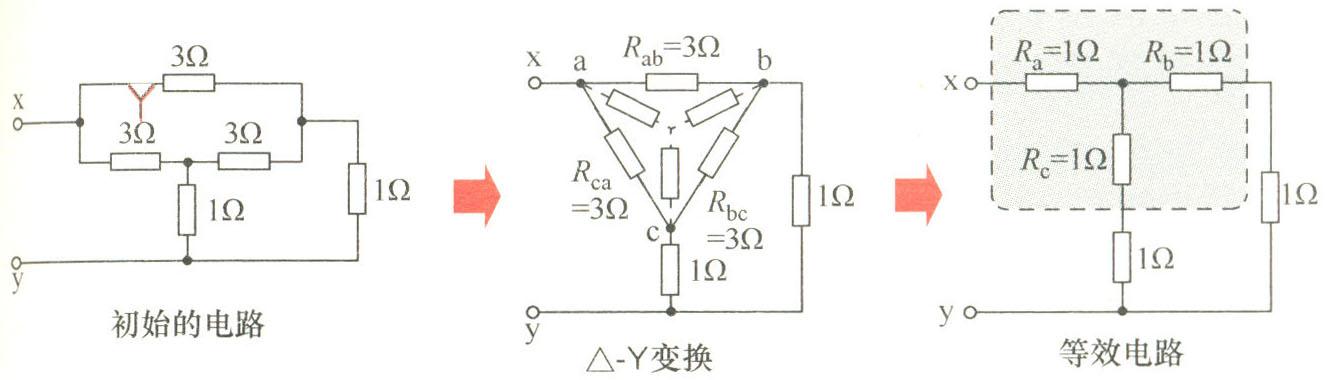
计算上面左图的电路xy间的复合电阻R0
首先,进行△-Y变换,Ra=Rb=Rc=1/3Rab=1/3*3=1,将初始电路变换为上面右图中的等效电路后,该串并联电路的复合电阻R0()就很容易计算了。
R0=2
1)等效电路的应用
通过等效变换,将电路A中的电阻用另一个电阻来替换,得到电路B。由于在等效电阻中流过的电流和其两端的电压相等,其消耗的功率也不变,因此电路A与B是等效的。通常,通过将电路中实际连接的电阻通过等效变换,会使得等效电路的分析和计算变得更为容易和方便。因此,为了简化电路的计算,等效电路的转换经常被采用,使得计算变得很方便。
2)△-Y变换
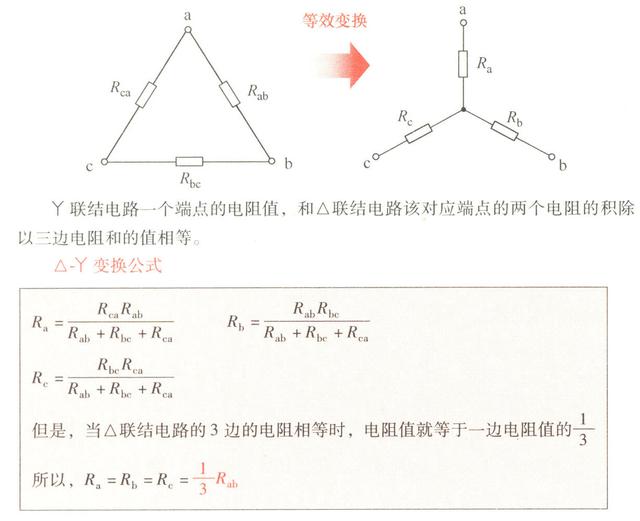
对于具有a、b、c三个端的电路,△联结电路中的三个电阻分别为Rab、Rbc、Rca。将其转换成Y字形接线电路后,Y联结电路中的电阻分别为Ra、Rb、Rc。这个变换过程即为△-Y变换。
3)△-Y变换的特点
当电路中包含有△联结电路时,直接采用串并联电路的计算方法是不可以的。在这个情况下,通过△-Y变换,得到的等效电路从a、b、c三个端来看,电路都是等效的,而变换为Y联结电路的话,通常就可以直接采用串联电路的方法进行计算。
4)△-Y变换公式的推导

从Y联结电路到△联结电路的变换(Y-△变换)
1.从Y联结电路到△联结电路的变换(Y-△变换)
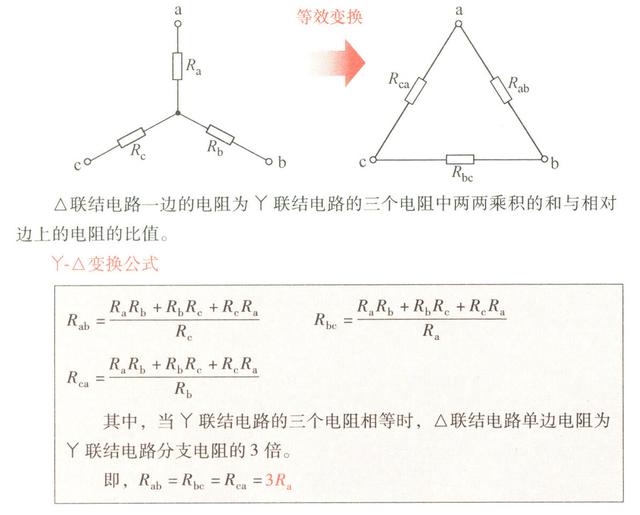
2.求变换公式所采取的方法
因为原来的电路为△联结电路,需要进行未知电阻Rab、Rbc、Rca串并联电路的处理,这样计算起来稍稍有一些复杂。如果按照下面的方法,稍加一些变换,计算就会更加简单。
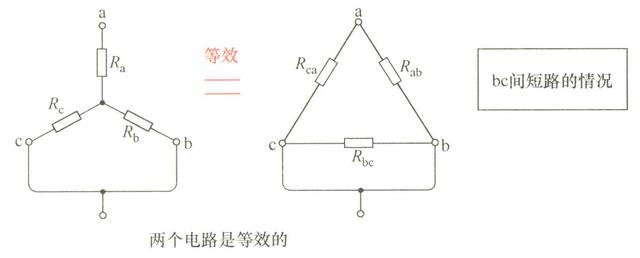
1)Y-△变换
对于具有a、b、c三个端的电路,Y联结电路中的电阻分别为Ra、Rb、Rc。将其转换成△联结电路后,△联结电路中的电阻分别为Rab、Rbc、Rca。这个变换过程即为Y-△变换。
2)Y-△变换的特点
Y-△变换在电路中乍看起来很复杂,电路复合电阻的计算常常会用到Y-△变换。虽然计算过程与△-Y变换有所不同,但我们还是可以用△-Y变换公式相同的方法,来理解Y-△变换公式。
3)Y-△变换公式的推导
将等效电路的Y联结电路以及△联结电路的bc两端短路(△联结电路是单一的并联电路)。由于两个电路为等效电路,所以a端与短接点之间的合成电阻的倒数(导纳)也是相等的。

不知道您是否看懂了呢?下面通过几个练习题来检验一下吧!
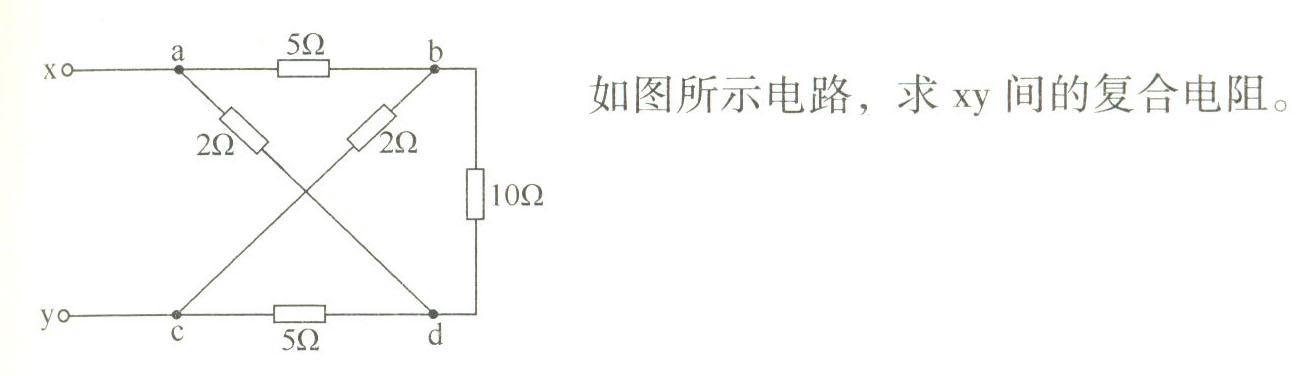
习题1
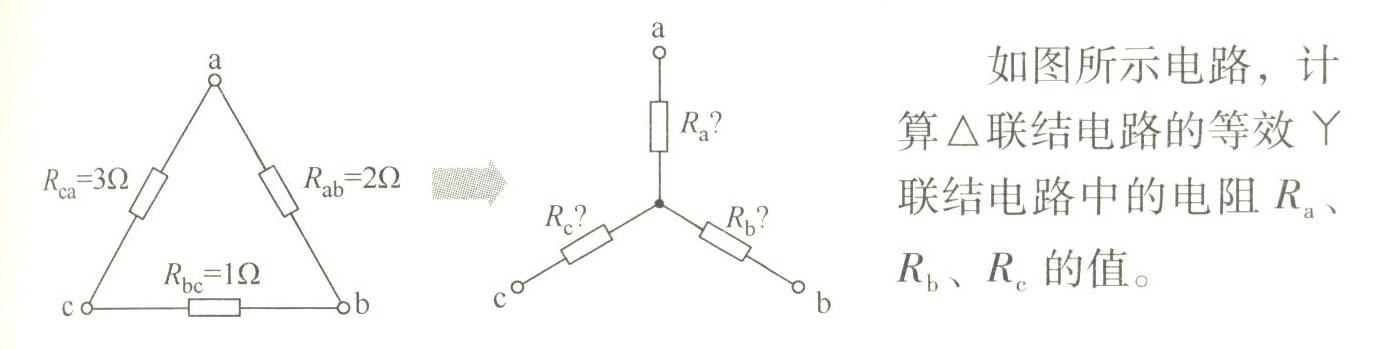
习题2
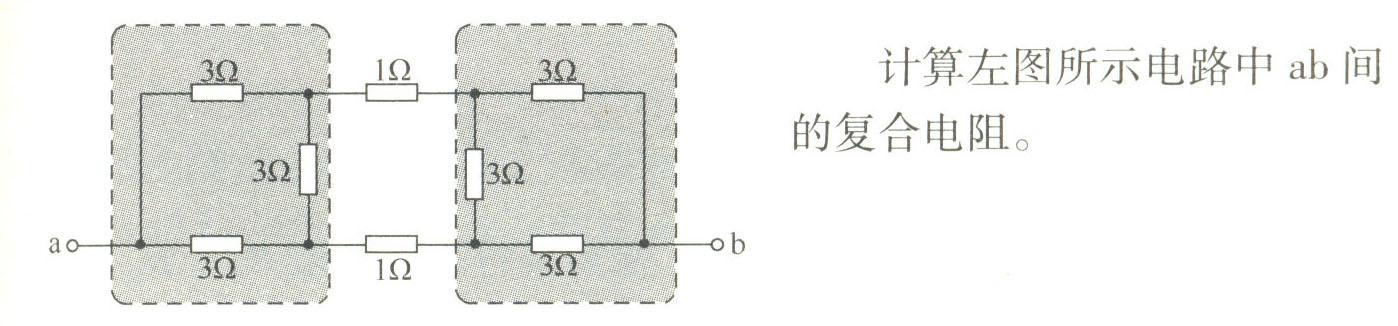
习题3
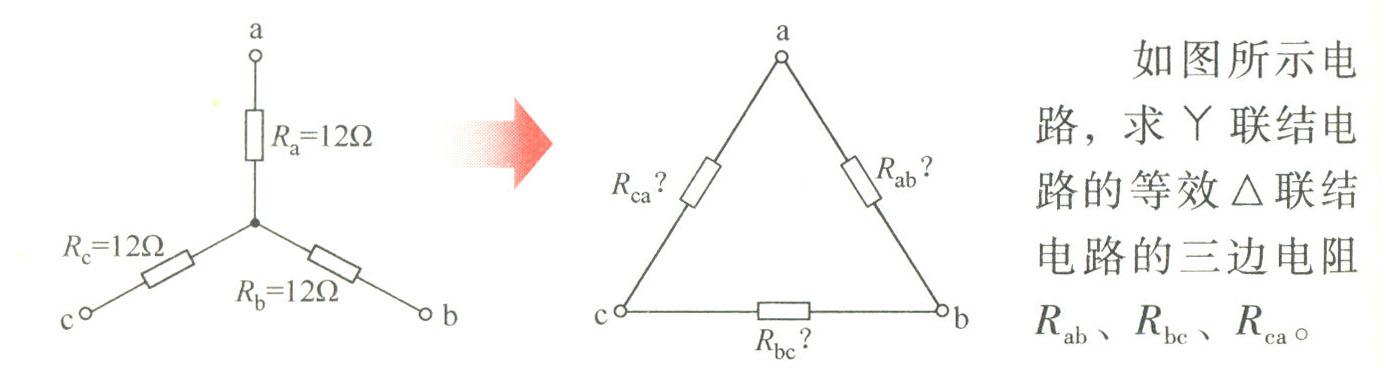
习题4