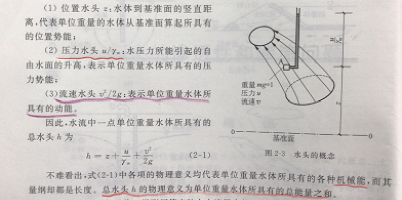
测管水头包括位置水头、压力水头和速度水头。为了简化,我们把位置水头和压力水头称为势能水头,速度水头称为动能水头。也就是说测管水头为势能水头和动能水头之和。
因为土中渗流水流的速度很慢,往往动能水头忽略不计了。其实达西定律就是忽略了动能水头,但本文仅仅是概念思考,所以我们可以不进行忽略,分析下水穿过土样流动是个什么规律。
我们再仔细观察下这个实验装置:

对左侧水杯放大如下:
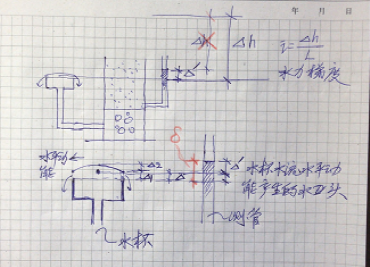
假设砂土密度减小一倍,水流速度一定会变快,这样水杯的出水的弧形平均高度△一定会变大,较大时或如喷泉一般冲出水杯(达西定律实验应该不包含这种情况,但因我们仅仅是概念思维,就可以展开想象了)。同时水平流速也会变快,相应的测管中的流速动能水头△也会变大,这样测管水头距量杯杯壁边缘顶部的高度地基基础设计思考与实践-水力梯度的探讨_5将变大,变大的幅度和土样的密实度有关。当水流是几乎喷出水杯时,其流速动能水头△占比也一定很大。
达西定律的计算公式:
从教材的图片上看 △h为稳定渗流中的计算点的测管水头差。从严密的定义上来说,测管水头应该包含水流速度能量产生的水头。但计算渗流速度时△h应不包含速度能量能产生的水头△。当然达西不会不知道这一点,只是因为实际工程中的土样中的渗流速度很慢,几乎可以忽略,故测管水头差近似于势能水位差。达西定律在工程上采用测管水头差来计算其误差不影响工程应用。
但教材中这个所谓的测管水头差损失的叫法是有歧义的,容易让人产生误解。损失汉语词义为:因什么原因造成了受损的结果。而对与土样的渗流来说,是因为土体的阻力,造成了测管水头的损失,本来自由落体中的水的测管水头差是没有损失的(全部由势能水头变成了动能水头)。
当土样密度很大水渗流速度很慢时,测管水头差和势能水位差数值上很接近。也可以这样理解,土样的渗流阻力消耗了水自由落体时的绝大部分动能,使的本来应该由势能水头变成的绝大部分动能水头的被土体吃掉了,所以从数值上势能差和测管水头损失相当(忽略微小的动能部分),但计算水力梯度的△h逻辑上应该叫势能差而不是测管水头损失。
要特别注意这个达西实验装置造成的一个问题是:因土样密度变化影响到水流的速度使水杯的向外溢流的平均厚度△变化,使土样上下端的水位差有所变化,这个水位差的变化又反过来又影响到了渗流速度,是果又影响了因,互相影响并达到稳定渗流的动态平衡。但这是因为实验装置的造成的,并不是必然的,而且这个装置造成的微小的果的差别变成的因,其影响很小,可以忽略不计。所以文十三中的那句类似哲学逻辑判断的话:水的势能差△H和土的渗流特性k是渗流的因,而测管水头△h差为果。以果计算果其结果肯定是错误的。不能说是不对的。
如果水对砂石土样的冲刷,带走了细颗粒,留下大孔的砂石,造成渗流速度极快,甚至有加速度,达西定律的测管水头包含的速度能量产生的水头很大,测管水头中的动能水头不能忽略时,应该用势能差来计算水力梯度,而不能用测管水头差计算水力梯度。
我估计岩土工程师在进行渗流计算水力梯度时应该用的就是水位势能差,而不是测管水头差。
另外,因为自由落体中的水,随着落体的高度不断的增高,其单位体积的水的质量在逐渐减小,就如黄果树瀑布一样,瀑布越往下水越稀薄,这和我们岩土中的渗流似乎不一样,因为渗流量是按水流速度计算的,不考虑水的稀薄。但从纯粹思维来说,大孔的砂石土样的水也可能发生加速流动的可能,这时候的达西定律是什么呢?当然这已经完全超出了本文的范畴,是否是岩土专业需要研究的,笔者不敢妄言。
