关于这方面实际的案例,有关的资料不是很多,也比较零散,规范条文有一些,但概念上不是很清晰。笔者不是搞科研的,很难得到一手实际工程的实测资料,对于上部结构的刚度的影响也只是用市场上的软件对比计算,但程序本身的技术内核无从知晓,无法真正判断其正确性,所以只能从概念上进行判断思考,和资料上的有关的数据进行对比。方向对的,对自己思考的概念可以证明其正确性,对与概念不符的,继续深入思考,会发现概念错误,但也可能会发现规范和资料等存在一些问题。
一:柔性荷载与刚体基础荷载对地基变形的影响
规范地基变形的计算公式如下:

公式是根据布氏的弹性半空间体的假定给定的应力系数,但因为应力系数是通过面荷载的积分出来的,所以本质是柔性荷载作用下的应力系数。
实际建筑无论是高层的筏基箱基或独立基础,荷载均是介于柔性和刚性之间的半刚性(与上部结构与基础的共同刚度有关),那刚性荷载对沉降的影响有多大呢?
下图是完全柔性荷载、完全刚性荷载、有限刚性荷载的基底反力(或结构对地基的作用力)和地基变形示意图。
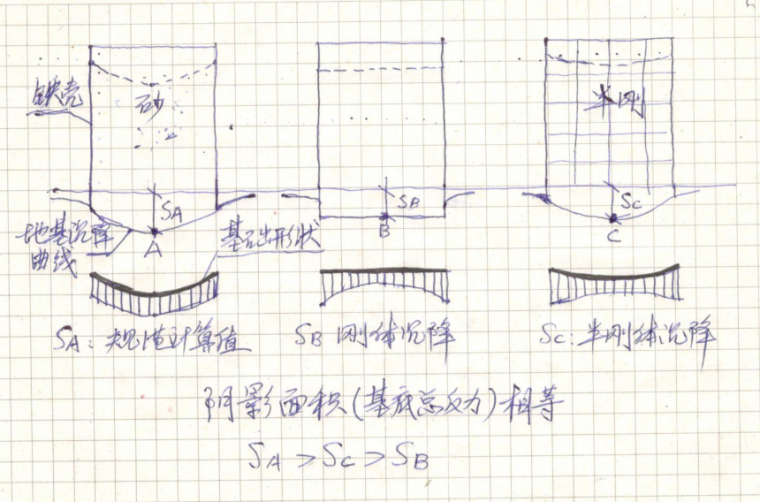
地基规范变形公式计算出的是A点的变形,B、C点的变形理论上如果知道了地基反力的分布,就可以根据布氏解积分计算出来,但我们无法准确的知道反力的分布。反力分布和地基变形是互相关系的,就像有两个未知数,我们只能列出一个方程一样,无法用规范的公式计算。
但通过很多的实际工程大致知道半刚性的建筑的地基反力分布和变形基本是上图右侧的图形。
现假设一个案例,算下三种情况各点的变形,进行下对比。为了概念清楚,采用规范的基本的公式计算,不用软件。

算例中平均变形是把柔性荷载的不均匀变形拉平,可以认为是刚性基础的变形,不过似乎有点想当然。
实际任何结构,上部与基础的刚度均为有限刚,建筑荷载均匀的情况下,中点的变形一定比边缘大。但边缘的地基反力一定比中部大,《高基》的高层建筑的地基反力的分块实际是考虑了一般高层建筑上部结构、基础与地基共同作用下的地基反力的情况。现按规范做一个变形算例。
下图为上述例题的同样条件的一般高层的地基反力系数,总荷载两个例题是一样的,平均值均为150KPa。
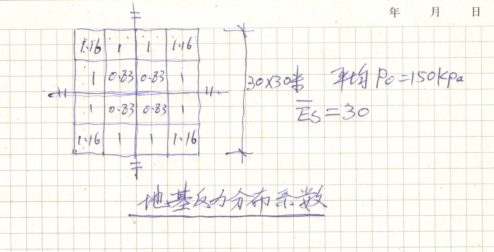
手算三个点的变形。
因为上述的地基反力的分布系数每块是不同的,所以必须分9块进行叠加计算。中点C的计算如下:

边缘中点的变形计算如下:

基础角点A点的变形最繁琐,过程从略。

三种情况变形对比如下:
(1)按规范的柔性荷载,中心点113.6mm,边缘中点65.2mm,角点40.5mm。刚性基础强制平均为89.4mm,刚性基础变形是柔性计算的79%。
(2)按《高基规范》给的地基反力分布系数,计算考虑了上部结构刚度影响,三点的变形分别为:103.36、64.8、40.5mm,中点沉降计算值是柔性荷载的91%,规范采用的柔性荷载计算和实际考虑上部刚度计算的变形相差不大。
本例题做了大的简化,具体数值虽然不具有实际工程的参考价值,但作为刚性和柔性的对比是有意义的。本结论与朱丙寅大师的《建筑地基基础计算方法与分析》的刚性基础沉降值是柔性荷载(规范公式)的80%的论述基本一致。
(3)按规范柔性荷载计算的地基变形偏于保守。但规范给于了公式很宽泛的经验系数,对于强条规定的变形控制值不同的结构采用不同的数值及方法,经验系数和控制值是大量的概率统计及计算对比得来的,这些来源于实际的数值和经验系数应该已经包含了上述的柔性荷载与实际计算的误差了。
二:基础形状和计算深度对地基变形的影响
总荷载相同采用方形基础和矩形基础进行对比计算及不同的计算深度进行对比计算如下:
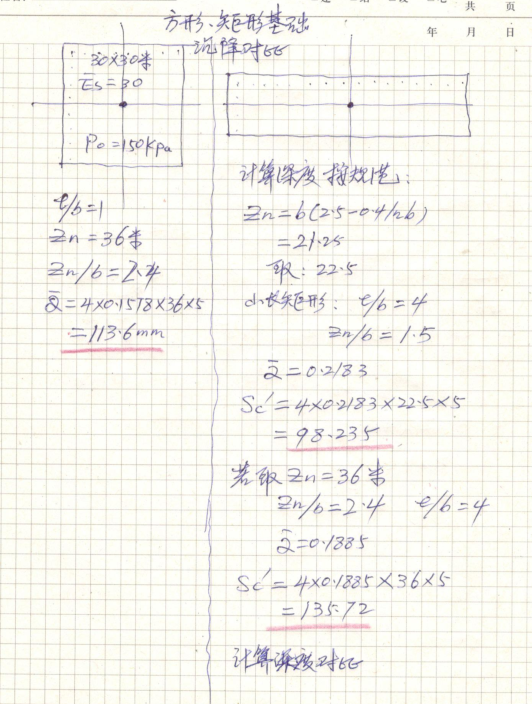
从算例可以得出如下结论:
(1)当总荷载相同时,方形基础比矩形基础沉降大。朱大师的《建筑地基基础设计方法及实例分析》中论述方形基础沉降比矩形基础小很多,所以一般基础应该采用方形基础的结论有误。

图2.3.11条形基础和方形基础实际是当基础平均反力相同时,无限长的条基和方形基础的对比,图形来源于布式解的推导,不是独立基础的矩形和方形的对比。
之所以大部分做方形基础不是因为沉降,而是因为方形简单。若一个方向有弯矩另外一个方向没有时,做矩形基础更经济,沉降也小一点,但形状对沉降的影响很小,可以不考虑。
(2)计算深度的影响应重视。理论上计算越深沉降越大,但完全按规范公式计算时未必如此。刘金波博士的《建筑地基基础设计禁忌和实例》中提到这一点。当不考虑修正系数时,深度越深沉降自然越大(这是概念),但若考虑沉降系数时有可能计算越深反而沉降越小。

我是这样理解的:首先说我们的概念没有错即计算深度越深沉降越大,出现这种情况的原因是修正系数不能包括某些特殊情况,这是没有办法的事情。所以要最好严格按规范的计算公式确定计算深度和修正系数计算,不能任意加大计算深度。
(3)对于规范5.3.8规定的简化计算深度,一定要正确理解,否则可能犯较大的错误。

这个简化的深度计算一定是无相邻荷载的影响才可使用。绝大部分情况是有相互影响的,除非独立的单体建筑的基础。有人在利用角点法计算中点沉降时,按分块的小矩形的宽度计算影响深度,算出的沉降太小了,就是忘记了相邻荷载的影响的先决条件。
对于结构独立基础之间一般距离较远,是否考虑临近荷载的影响,很难判断,所以还得用规范公式计算深度向上一定深度的沉降小于总沉降的2.5%来判断,这个是影响深度计算的基本公式。用简化的公式一般应该用它来校核。对于复杂的互相影响的基础沉降计算深度的确定太繁琐,必须依赖于计算机。
(4)刚性下卧层的对沉降的不利影响
计算地基承载力时,需要计算软弱下卧层的承载力。在本系列的(三)中讲过,当土层上硬下软时,上层土的应力扩散较快,所以采用较大的扩散角,反之采用较小的扩散角(见系列三)。
所以规范对于有刚性下卧层时比如岩石,沉降计算深度可以到岩石顶面,但要考虑上部应力扩散角变小的不利影响。地基规范6.2.2第二条即是考虑了刚性下卧层对沉降变形增大的影响,很多人未必注意到这一点。

三:基底反力不同对地基沉降的影响
1、圣维南原理
圣维南原理(Saint Venants Principle)是弹性力学的基础性原理,是法国力学家圣维南于1855年提出的。是弹性力学中一个说明局部效应的原理,虽然已经有大量实例验证,但至今还没有严格证明。其内容是:分布于弹性体上一小块面积(或体积)内的荷载所引起的物体中的应力,在离荷载作用区稍远的地方,基本上只同荷载的合力和合力矩有关;荷载的具体分布只影响荷载作用区附近的应力分布。
原理要点:
一、进行替换的两个力系必须是刚体力学的等效力系;
二、力系替换的表面必须小,在替换表面附近的解失去精度。
意义:
圣维南原理在实用上和理论上都有重要意义。在解决具体问题时,如果只关心远离荷载处的应力,就可视计算或实验的方便,改变荷载的分布情况,不过须保持它们的合力和合力矩等于原先给定的值。圣维南原理是定性地说明弹性力学中一大批局部效应的第一个原理。
同样,建筑基础作用于地基上时,在地基表面及附近的应力因为上部结构的刚度、荷载、基础的形式等复杂的因素,造成基底反力(也是基础施加在地基上的荷载)比较复杂,但在离地基表面较远的地方,基本只和荷载的大小及合力矩有关,这一点地基也同样适用。
但地基土因为离散性大,强度比较底等原因,可能这个局部的范围较大,但通过上述的计算分析,这个局部范围的影响大概约10~20%的误差。也就是说按规范公式计算的沉降和实际有一定刚度的基础沉降相差不大于20%。
2、圣维南原理也说了,对于荷载作用点的附近局部范围内其应力变化无法精确求解,所以对于地基表面与基础接触的部位不能用布氏解的应力系数来求解。
比如:规范附录给出的地基附加应力系数,在深度为0处角点的应力系数为0.25,见下图:
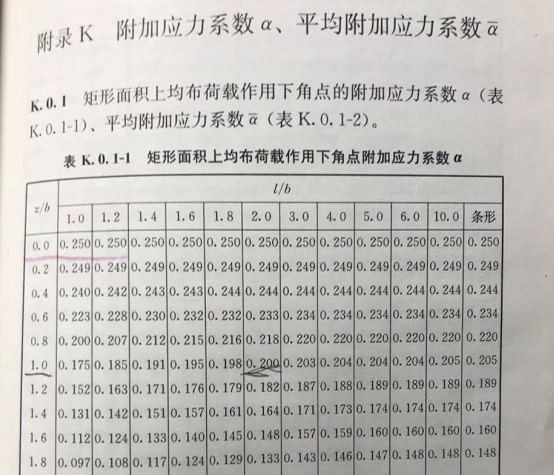
如果按这个计算,在地基表面处,柔性荷载的中心点的应力(地基反力)应该是角点的4倍,但其实地基反力和结构柔性荷载完全相等(见上文中草图),否则就违反了牛顿第三定律力的平衡原理了。
也就是说布氏解也无法解答地基荷载作用面附近范围的应力计算,只有在一定深度的范围才能应用布式解即规范的附加应力系数。
实际工程地基地基的压缩深度一般应该在超过了这个有限的范围了,所以不存在上述的不能解答的问题,但不同的分布应力的确只在较浅的范围有影响,这个影响大概就是上面所说的10~20%的范围吧。
四:大底盘结构的地基沉降的计算
《地规》5.3.12和《高基》5.4.5、5.4.6都提到了上部结构、基础、地基的共同作用以及大底盘的多塔楼的沉降计算问题。但太笼统了,很难具体操作。
根据上面的分析及本系列以前文章的论述,笔者建议如下进行:
1、对于单体高层建筑,现在的软件已基本可以计算考虑结构和基础的刚度了。对三者共同作用求解地基反力进而进行地基沉降计算,如果地基参数完全相同,上部结构及基础模型正确,计算结果应该和上述算例中的分块叠加法相当。但整体建模很难完善,而且计算结果设计人很难把握,概念不清不易判断。
建议高层建筑按规范公式进行单体沉降计算,可按《高基》规范的地基反力分布图进行分块叠加计算。一般多层建筑的筏板基础可直接按规范公式计算沉降及倾斜,当层数不同时按层数划块计算叠加。独立基础按规范公式计算沉降及倾斜,但要考虑不同独基之间的影响。
2:对于框架核心筒等结构,其核心筒因自重大,恒载与活载准永久组合大于周边框架时可以井筒为区格,并参考《高基》进行分块考虑不同的反力分布系数进行计算。
3:对于高层塔楼和周边裙房,可以塔楼与裙房交接线划分区块,进行叠加计算。裙房划分的依据,以裙房的层数不同而划分,高层塔楼的划分见上文。
4:当裙房为多层框架时,对于筏板基础可以采用整体划分,对于独立基础可以以独基为分块划分。对于刚度很弱的防水板基础建议按适当扩大的独基来分块。
5:分块叠加计算沉降手算几乎无法完成,建议开发分块计算的小程序,便于工程师灵活进行分块,这样概念清楚容易控制进行对比计算。实际工程往往底盘形状复杂,难以划分规矩的矩形,见下图某实际项目简图:
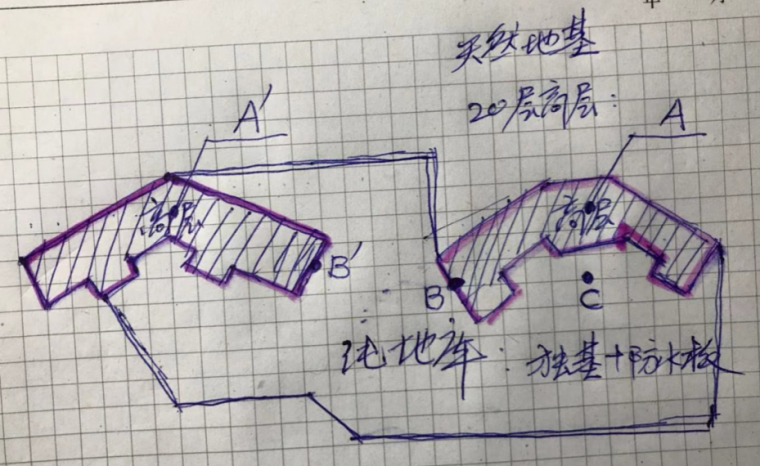
基础不能划分成规矩的矩形区格,所以不能直接应用规范的附录中的附加应力表,但程序可以开发出任意形状区格(比如三角形等,用布氏解积分)的附加应力系数还是比较容易的。
6: 采用划分区块叠加的计算方式根据有关资料证明是符合工程实际要求的,不必要求必须三者共同分析计算沉降。三者共同分析得出的地基反力可用于基础本身的计算,因为其对基础的影响比对沉降的影响大的多。
四:对规范倒楼盖计算要求地基梁刚度(1/6跨高比)的疑问
1、上部结构的刚度基本决定了结构竖向构件根部的沉降,见下图:
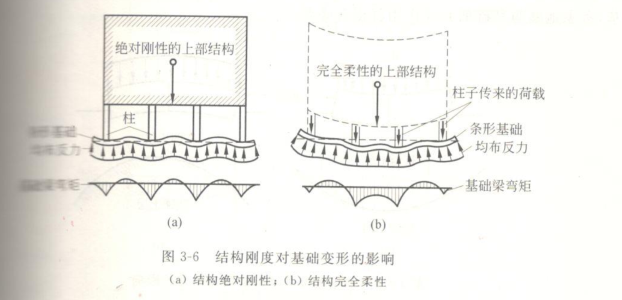
基础梁的刚度虽然可以使竖向结构的根部的沉降差更小,但因为仅为一层梁(虽然比楼层梁大很多)所以起的作用并不大。所以对于上部结构刚度非常大的结构,基底反力的分布是大水平,小波浪。地基梁越刚,小波浪越接近水平。
起伏的小波浪的分布力实际减少了梁的弯矩,用倒楼盖水平的反力进行计算是偏于保守的,当上部刚度足够大时,不必追求1/6的梁高即可用倒楼盖计算,满足地基梁的规范的各项要求即可。当然刚度大的地基梁使地基反力更均匀,可以降低沉降,但上文分析可以看出,这个有利的影响实在微乎其微。
2:若上部结构为比较柔的框架时,为了采用倒楼盖计算法,按1/6确定基础梁断面,地基梁做的很大很浪费,但整体弯曲仍然很大,采用倒楼盖是不安全。是否应用倒楼盖法的关键是上部的刚度。若基础梁做的刚度很大,虽然小波浪比较平滑了,但整体弯曲仍然很大(单层的基础梁毕竟无法与很多楼层的梁的刚度相当),这时采用倒楼盖是不安全的,应该用考虑上部结构、基础、地基者共同作用的弹性地基梁法计算。但有资料显示,共同分析的弹性地基梁的钢筋应力远远小于计算配筋的应力(几十分之一),资料认为是基底巨大的摩擦力减少了基础梁的整体弯矩的轴力造成的。
五:手算地基变形的体会
本文手算的例子虽然简单,但花费的时间不少于4个小时,发在超限群的第一稿的计算结果还是漏了重要的一环,只好修改参数又重新算了一遍,好在最复杂的应力系数的合与分没有错。在计算过程中几乎没几步就要出错,原因是查应力系数表、划分9块,分分合合极易出错。每次出错之所以能够发现主要是靠的是概念正确,比如应力扩散,远近、方形或矩形形状、面积大小的影响等,如果概念不清,几乎结果必然为错。上述算例是否完全正确,还希望各位专家验证。
从这里也可以看出,即使已经进行了大量的简化的案例,还如此容易出错,花费的时间也很长,不能被现在的高效率所允许。所以实际工程中对于复杂的互相影响尤其是多建筑大底盘的基础计算手算沉降非常困难,几乎做不到。但这种方法的概念很简单,利用计算机的优势用这种分块叠加的概念应该是不错的方法。
本文上述纯粹是概念分析,仅供有关技术人员参考。有很多设计人对地勘的参数表示怀疑,本文不进行讨论。本文着眼于结构师需要考虑的部分,做好我们自己的这摊事儿,岩土参数是岩土工程师需要负责的,大家是一个联合部队,只是军种不同,需要各自负好自己的责任,共同配合、互相学习沟通,才能打胜仗。
