桥梁概况及方案比选 西部某高速公路干线连接线上某桥是该连接线的主 线桥,本桥所在路段推荐方案(以下简称K线方案)为, 线位位于缓和曲线长LS=40m,半径R=35m,缓和曲线长LS=25m的平曲线内,纵坡为4.7%,横坡为5%。桥 梁 主 要 尺 寸 及 技 术 标 准 为 :全 宽 - 1 0 . 4 m , 净 宽-9.4m,现浇梁高125cm,沥青混凝土铺装厚10cm,设计 车道数按照两车道计算,7度设防地震烈度。(K线方案如图 1:路线方案示意图)
1.1 桥位总体方案定性比选
在项目初期考虑到K线方案的半径较小,增加了一个扩大半径后的方案进行比较。首先用定性比较的方法,对增 大半径的方案与K线方案进行比较。桥梁所在路段有旧路,旧桥桥位在本桥两方案上游, 旧路为28m半径路段中以1~8m小桥跨越本沟,两方案沟底 处纵坡均为12.5%。将本路段圆曲线半径加大后形成一个圆曲线半径为55m 的路线方案(以下简称55m半径方案),本路线方案为半径 增大的极限,如继续扩大圆曲线半径,工程量会明显多于K 线方案且实施难度会大幅增加。K线方案与55m半径方案在 平衡工期与造价之后,定性比较如下:
⑴因为本路段是受纵坡控制的持续上坡路段,按照K线 方案桥梁段前后已接近极限纵坡。如果按照55m半径方案实 施势必会造成桥梁纵坡增大。经过测算,路线每减少10m纵 坡要抬高0.656%,而如果半径加大到55m,路线会至少减 少20m,纵坡会达到6%左右,于结构物设计难度、施工难度与工期都会有较大影响。
⑵55m半径方案的线位在K线方案过沟位置的下游方向 约26m处,K线方案布跨选用15m跨径,需要4跨,平均墩 高约为10.3m,而55m半径方案选用13m跨径,需要5跨,桥墩处对应填土高比K线方案增加3.25m左右,平均墩高约为 13.55m。虽然55m半径方案较K线方案路线长度会减少20多 m,但是由于提高了路线指标,甩开旧路路基路段的造价会 大幅提升。在这部分增加的造价比较下,因减少路线长度 而减少的工程量几乎可以忽略不计。桥梁工程中,55m半径 方案桥墩墩身造价比K线方案提高约31.5%,而上部构造并 不会因为增大路线半径的同时,减小桥面面积而使造价减 少(桥长反而增加了),本方案也不能使用统一模版预制 上部梁板以减少工期。
综上所述,经过定性比较,增大半径的方案对于本 座桥梁来说不仅不会节约预算,而且会延长工期;另一方面,K线方案中的35m半径圆曲线,以通、顺的连 接支线在做好其他行车安全保障措施的基础上,线型指标 是完全可以接受的。
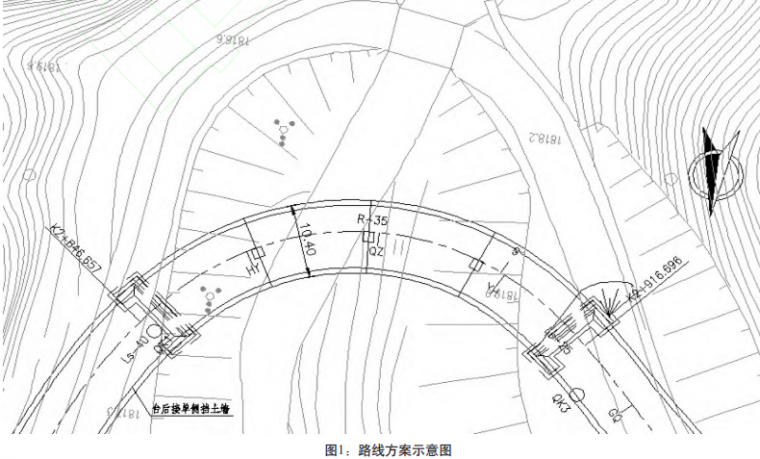
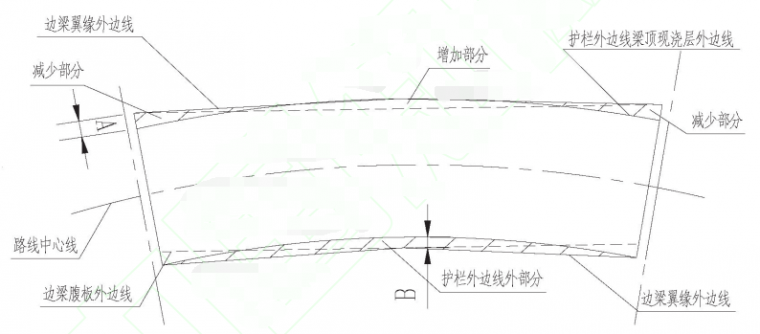
图2:边梁翼缘板及现浇层平面变宽示意图
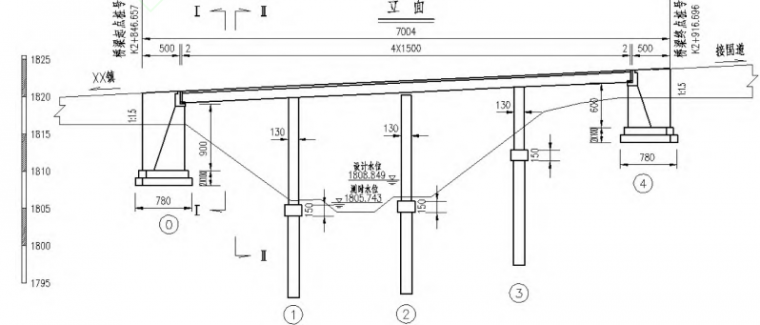
图3:桥型推荐方案立面图
1.2 桥型方案比选
针对K线方案,还应进行不同桥型方案比选。
1.2.1 上部结构比选
鉴于桥梁所在路线圆曲线半径较小,相对来说使用 13~15m跨径桥梁最为合适。这主要考虑了三个方面的因素。
⑴在路线线型为小半径的情况下,如采用弯桥直做的 预制结构,平曲线型由护栏在外侧调整实现(方案示意图 见图2),考虑到悬弧差会根据跨径增大而增大,若悬弧 差较大则会造成材料浪费以及线型不顺畅,故跨径不宜过 大,且本桥主跨跨径不受河道与流量的制约。
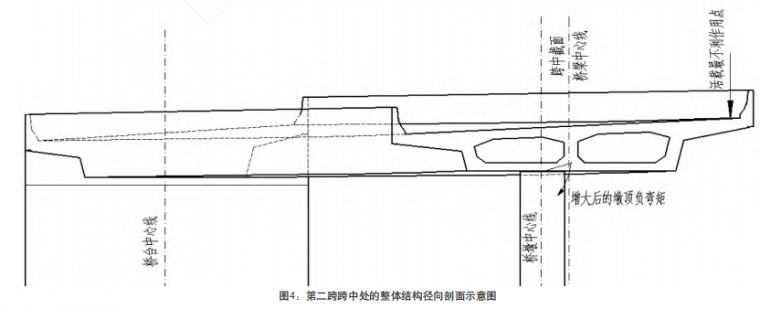
⑵若采用现浇箱梁作为上部构造,跨径越大在跨中位 置的形心距相邻两桥墩台理论支撑点连线的距离(形心位 置大致等同桥梁中心线位置,如图4中跨中截面桥梁中心线 到桥墩中心线的距离)也会越大,对抗扭刚度会有更高要 求,造成造价增大,跨径过小又会造成下部材料浪费。
⑶采用现浇连续箱梁时,随着小半径桥梁跨径的增 大,则箱梁势必需要使用预应力实现抗弯能力。对于本 路线方案,抗弯预应力索由于按照曲线布置,桥梁单跨 跨径越大,其产生的径向分力越大,则对抗扭性能产生不 利影响越大,根据小半径桥梁特点尽量降低梁高,并 且尽量减小抗弯扭刚度比(即减小抗弯刚度,增大抗扭刚 度);同时如现浇连续箱梁跨径过大还要考虑采用独柱偏 心墩,用以平衡恒、活载偏心作用而导致的扭矩增大、翘 曲形变与外侧腹板弯扭的耦合效应,由于两者都会非线性 增大、翘曲形变也会引起翘曲正应力并伴随剪应力出现以 及双支座时可能产生的半径内侧支座脱空的现象。综合考 虑上述问题后,曲线桥的跨径最好不要过大,以15m跨径最 为适宜,而更好的办法就是尽可能采用普通钢筋混凝土结 构,避免使用预应力,同样这种办法也是以跨径不能过大 为前提的。
综上所述,本桥上部结构拟定两个方案:方案一:513m预制钢筋混凝土空心板方案,U台、扩大基础,桩 柱式桥墩;方案二:415m普通钢筋混凝土现浇连续箱梁 方案,U台、扩大基础,固结独柱墩、独柱墩、桩基础(方 案二见图3)。
1.2.2 上部方案比选
根据前文的论述,这两个上部结构方案本身是有理论 依据的,并且是有比较价值的。具体比较如下:
⑴方案一特点 由于全桥都位于平曲线段上,因此采用主梁调整预制 长度,如图1所示,空心板翼板的宽度根据曲线半径确定 预制长度;因为每跨梁长的不同,所以在结构计算及配筋 时,需要根据梁长的差别按照不同梁长级配计算配筋,这 样缺点是:
①设计阶段设计周期会增长;
②实施阶段会因为增多了模板套数而抵消预制结构原 有的节省工期以及比现浇结构节省造价的优势;
③运营阶段上部结构还会由于横向不同、梁板板长和 刚度不同更易在铰缝处形成通长裂缝,影响运营期的使用 以及增高养护成本。
⑵方案二特点 同样全桥位于平曲线上,现浇结构可以避免方案一 所叙述的问题;采用较小跨径而实现的普通钢筋混凝土结 构,避免了预应力的径向分力对结构内力以及对抗扭性能 的影响。对于曲梁在外荷载的作用下会形成挠曲变形与弯扭耦 合共同变大的情况,但对于受力模型来说还是跨中下缘形 变与耦合更严重,普通钢筋在这个位置随变形增大而增加 使用效率,同时提供了更好的抗弯扭和对抗翘曲正应力的 效果。根据结构受力分析比较,在15m跨径的35m半径时,内外腹板跨中处弯矩较内外腹板弧线长度对应跨径的直桥跨 中弯矩数值相近,故可以简化为根据内外腹板弧长的直桥来进行替代内力计算,从而减短设计周期;由于桥面横坡为5%,梁底为平坡,半径外侧腹板比内 侧腹板高,这正符合了内外侧抗弯与抗扭的区别,客观上 降低了一定的梁高;腹板采用钢筋骨架配筋增加整体性、抗弯能力、抗扭 能力,同时也对翘曲形变引起的翘曲正应力及其伴生的剪 力有一定抵抗能力。
经上述比选后上部结构选用方案二,这个方案在构造 合理性、全寿命工期及经济综合评价以及上部结构具体受 力条件的改善方面都更为出色。
1.2.3 下部方案比选
通过上部方案比选,选定了普通钢筋混凝土现浇箱梁 的方案,下部结构就以上部本方案为基础,选择了两个方 案比选。
方案一:固结独柱墩、独柱墩、承台、桩基础,固结 独柱墩布置在1、3号桥墩(如图3),2号墩为独柱墩。
方案二:偏心独柱墩、承台、桩基础。鉴于桥梁所在 路线圆曲线半径较小且存在缓和曲线段,无法根据圆曲线 线形大、小桩号方向对称布置,以缩短设计、实施阶段周 期,故而全桥墩柱采用径向布置。上述方案的力学模型最大的差别在于,方案一活载作 用在径向剖面(见图4)上时,对结构整体产生的最大弯矩 较小。活载最不利工况力学模型的受力特点是:利用径向剖 面双侧桥墩以外的上部结构自重,平衡两侧桥墩内的恒载 及活载对相邻两桥墩墩顶主梁构成的负弯矩(如固结墩顶 同样有弯矩)。在综合考虑了两个方面因素后,最终推荐方案一,其 比较过程如下。
稳定性分析 :本结构采用了固结独柱墩与独柱墩相结 合的墩身结构,15m跨径对应中35m半径处的跨中最外侧可 能出现的受力点到此跨两独柱墩支点连线的距离为:5.0m (直桥为4.3m),差值为0.7m(如图4中跨中截面桥梁中心 线到桥墩中心线的距离),经计算在不考虑墩顶固结的最 不利情况下,也不会造成边跨半径内侧支座脱空的现象出 现,故而不需要利用偏心下部结构保证稳定性,否则方案 二势必会由于下部偏心结构而增加造价,就稳定性分析而 言选用方案一为宜。抗震及整体性分析:方案一与方案二在墩梁结合处的 区别是:以支座作为上下部结构过渡的墩身仅承受并向上 部结构传递了轴力、剪力,而固结墩除了传递轴力、剪力 外,同时还承受弯矩作用,有效的减小了上部结构的自由 度,提高了桥梁整体的抗震稳定性,并能有效防止纵坡过 大以及其他原因造成落梁。由于固结墩采用了矩形截面,所以主要是径向方向与 切线方向自由度较大,并且由于尺寸的原因桥墩给上部构 造增加的刚度很小。能更好利用桥梁整体的刚度对内力进 行再分配,以提高整体性。由此可见从抗震及整体性分析而言选用方案一有一定 优势。经上述比选后下部结构选用方案一。
2 设计要点
由工程实例总结的非匝道小半径桥梁设计要点。根据上文对工程实例讨论研究,在综合考虑造价和工期后,现将对于与上文中工程实例同类型项目的小半径桥梁(匝道桥除外)具有普遍意义的设计要点,特归纳如下。
2.1 桥跨布置及方案选定注意应结合布跨结果,布置固结墩的位置,以及非固结墩台的支座选用。一般情况下,二级及以下公路的小半径桥梁多是在陡坡深沟处,以路线贴近等高线走向以减小工程量。这种路段一般为缓和曲线加圆曲线加缓和曲线的形式。所以,一般来说在地形、水文条件允许的情况下,尽量在圆曲线曲中点附近布置一个桥墩,圆曲线所在的一联桥梁尽量以此桥墩为基准对称布置,可以最大可能的避免边跨半径内侧支座脱空,并且这种布跨方案在活载作用的最不利情况下(见图4)对结构整体产生的弯矩最小。
2.2 结构尺寸的方案拟定原则 在条件允许的情况下,尽量降低梁高,尽可能减小固 结墩墩柱的截面尺寸,增大桥墩的柔度,这样可以尽量减 小桥墩由于固结对上部结构内力的影响,并让下部结构在 由于上部结构翘曲形变产生翘曲正应力时更有效的参与内 力再分配,使结构受力更合理,项目投资更高效。
2.3 结构计算要点 结构计算要点包括:进行正常独柱墩径向剖面的上部 稳定性计算(边界条件按简支计算);采用偏心墩的整体 稳定性计算(边界条件按简支计算);如偏心墩无法完全 解决支座脱空问题,就需要进行固结偏心墩的整体稳定性 计算(边界条件在固结墩处采用固结计算)并且根据固结 界面不同情况进行截面配筋验算。
