笔者对TN - S系统接地故障保护的计算和验收进行了一些思考分析,供参考指正。
规范要求和阻抗法
GB 50054 - 2011《低压配电设计规范》第5.2.8条提出:TN系统中配电线路的间接接触防护电器的动作特性,应符合下式的要求:

式(1)与IEC 60364 - 4 - 41:2017《 Lowvoltage electrical installationsPart 4-41:Protection for safetyProtection against electric shock》中是一致的,U0和Ia都容易获取,难点是Zs的计算。GB 50303 - 2015《建筑电气工程施工质量验收规范》第5.1.8条,对接地故障回路阻抗的实测值要求满足式(2),并要求对20 % 的末级配电箱至少抽查1个回路:

式(2)与式(1)的差别只在于多了个2 / 3的系数,主要考虑实际故障时的导体温度比测试时导体温度高引起的电阻变化。式(2)与IEC 60364 - 6:2016《Low voltage electrical installationsPart 6:Verification》D.6.4.3.7.3中公式相同,只是IEC标准中允许测试结果不满足要求时用更精确的评估方法来作判断:外部阻抗Ze采用测量值(不考虑温度上升),而干线和末端线路的阻抗考虑故障电流引起的温升(不一定按2 / 3系数)。
BS 7671 - 2018《 Requirements for Electrical Installations》第411.4.4条、第643.7.3条和附录3也采用了类似的判断方式。不同的是BS 7671 - 2018考虑了电压降低的系数(常规为0.95),而温升系数采用0.8而不是2 / 3,两个系数相乘后实际为0.76,比GB 50303 - 2015的0.67略高。此外,BS 7671 - 2018对熔断器和微断不同时间切断的Ia给出了明确的取值,在测量值不满足条件的情况下,也允许更精确的评估。GB 50303 - 2015虽然测量值是唯一指标,但允许抽查会导致很大的人为因素。
要计算准确的阻抗值,需要采用将电阻和电抗分开计算的阻抗法。国标图集19DX101 - 1《建筑电气常用数据》表15.8给出了在一定假设条件下,不同型号规格的变压器、低压配电柜出线截面在10~240 mm2、10~150 m每整10 m处根据阻抗计算的单相接地故障电流值。这些表格对于第一段配电线路的长度验算非常有参考意义,实际工程根据具体情况修正后应用是没有问题的。
阻抗法是与规范要求最贴近、计算结果最准确的一个方法,在有条件的情况下应该是首选方案。目前第一段配电线路长度的查表是可行的,ABB的DOCWIN和西门子的SIMARIS DESIGN也提供了采用阻抗法的软件解决方案。
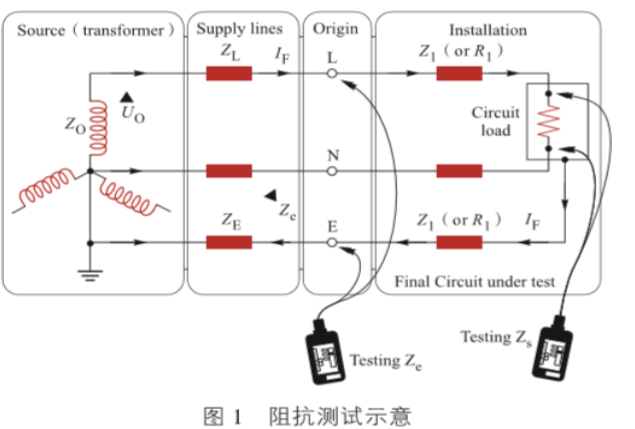
图1是《 A Practical Guide to the Wiring Regulations 》中阻抗测试示意。阻抗测试可用多功能电气测试仪带电测试,但仪器本身也有测量范围和一定的误差,现场线路绕行、接头、参数取值差异、测试误差等因素可能导致计算满足但测试不满足的情况。
简化计算公式比较
施耐德《电气装置应用(设计)指南》2017版提到了组合法和通用法两种简化计算方法,均是将阻抗分离的计算折算成电阻后算术相加,这样计算得出的电流偏小,保护元件动作更为可靠。
组合法比较少见,需要知道线路始端短路电流(或线路始端前折算成电阻的回路阻抗)。西门子《电气安装技术手册》(第2版)表1 - 7 - 29~32给出了一种末端线路长度查表的解决方式,这些表是根据导体种类、截面、保护装置类型、额定电流以及保护装置前的回路阻抗来获得回路的最大允许长度。表格比较复杂,也不够完整,虽然不用计算本回路阻抗,但需要知道外部阻抗,除了改造项目可以进行测量外,计算比较繁琐。
通用法源于IEC 61200 - 53:1994《Electrical installation guidePart 53:Selection and erection of electrical equipmentSwitchgear and controlgear》提出的一种工程应用简化和校验办法的实用公式。目前的专业书籍、手册和图集的相关计算公式看起来大同小异,也是因为它们的思路均是源于此公式。现在应用比较多的几个简化计算公式主要来自于施耐德《电气装置应用(设计)指南》2017版(以下简称文献[1])、ABB《低压配电电气设计安装手册》(第4版,以下简称文献[2])、《工业与民用供配电设计手册》(第4版,以下简称文献[3])和国标图集19DX101 - 1(以下简称文献[4]),由于不同资料中同类参数的字母表达不一致和篇幅关系,表1按实际参数在分子、分母的位置和大概的作用进行比较。
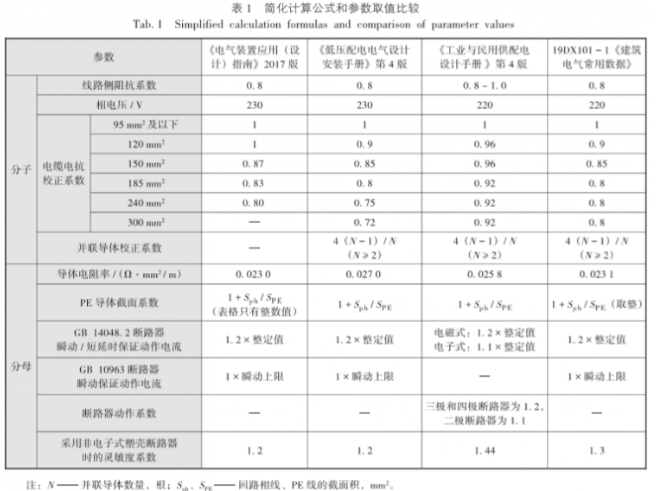
需要说明的是文献[1]第F章中铜的电阻率取0.022 5 mm2 / m,但根据公式和表格反算实际约为0.023 0 mm2 / m,与文献[1]第G章取值一致。
简化计算公式参数取值分析
导体电阻率
导体电阻率主要取决于20 ℃ 电阻率和对应的温度系数。根据GB / T 3956 - 2008《电缆的导体》中导体单位长度的电阻参数,反算20 ℃ 时2.5~300 mm2 绞合铜导体的最大电阻率在0.018 0~0.018 5 mm2/ m之间,这是产品的合格极限值。实际电缆产品并不是分别考核电阻率和截面,而是直接考核单位长度的电阻,电缆50 Hz交流电阻和直流电阻的差异较小。由于通用法公式只有一个电阻率,在计算最小短路电流时铜的20 ℃电阻率选用0.018 5 mm2 / m是比较合适的。
短路结束时导线温度由短路前导体的温度和短路电流在持续时间内产生的温升决定。如果在刚好满足断路器保证动作电流的情况下,接地故障电流在0.4 s内切除,铜导体最终温度可根据GB 50054 - 2011中公式(3.2.14)、公式(A.0.1)和表A.0.1的取值转化公式进行计算:

将几种常规的断路器和电缆组合参数代入公式(3),得到表2。
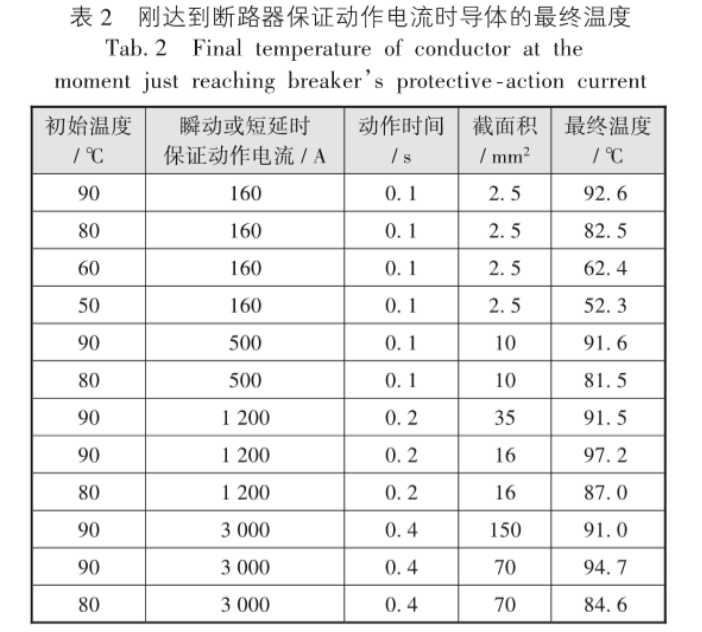
从表2可知,在刚好满足断路器动作误差极限的情况下,相线和等截面PE线的温升比较小,在3 ℃ 以内;而当PE线约为相线的一半时,PE线温升在8 ℃ 以内;相近条件下截面越大,温升越低。如考虑PE线平时无电流,温度比相线低时,整体基本可视为与相线初始温度一致。
短路前导体的温度为运行温度,可按IEEE Std 242 - 2001《Recommended practice for protection and coordination of industrial and commercial power systems》第9.5.2.2节公式计算:

根据式(4)对实际电流达不到额定电流的导体温度进行计算,结果见表3。
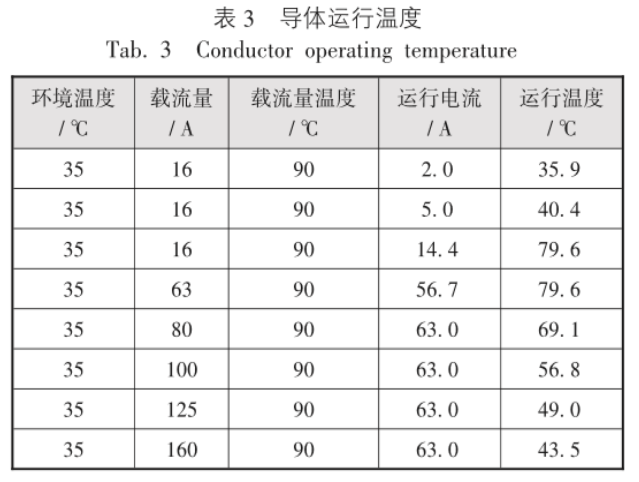
常规设计的情况下,运行电流为载流量90 % 时,90 ℃ 的导体运行温度约为80 ℃,但有两个地方需要特别注意:① 末端线路由于最小截面的限制,运行电流和导线的载流量有比较大的差别,实际运行温度会比较低;② 由于接地故障或者电压降等原因放大导体截面的线路,实际运行温度会比较低,而且截面放大以后接地故障电流引起的温升也会降低。在SIMRIS DESIGN中可以通过灵活设定计算最小短路电流的温度让计算结果更接近实际。
文献[4]的电阻率取值(温度系数取1.25系数,约82.5 ℃)和文献[8]的解释是比较合理的,特殊情况也允许更小的取值,但这样做会导致该回路被抽中时不一定满足GB 50303 - 2015。因为按GB 50303 - 2015验收时实测阻抗值乘1.5,即使在20 ℃的室温下空载测试也相当于要取1.5的温度系数计算才能保证通过验收。但设计无法控制验收测试的情况,如考虑夏季超过30 ℃时验收需要取比1.5更高的系数,该验收要求不是太合理。下文的分析以文献[4]的电阻率取值为参考值。
PE导体截面系数
这个系数的差别实际只有取整和不取整的差别,用Excel进行计算时取不取整基本没有难度上的区别,但这个结果对于误差来说影响还是比较大的,相对误差为 + 6.3 %~- 14.6 %(如表4所示),因此不建议取整计算。
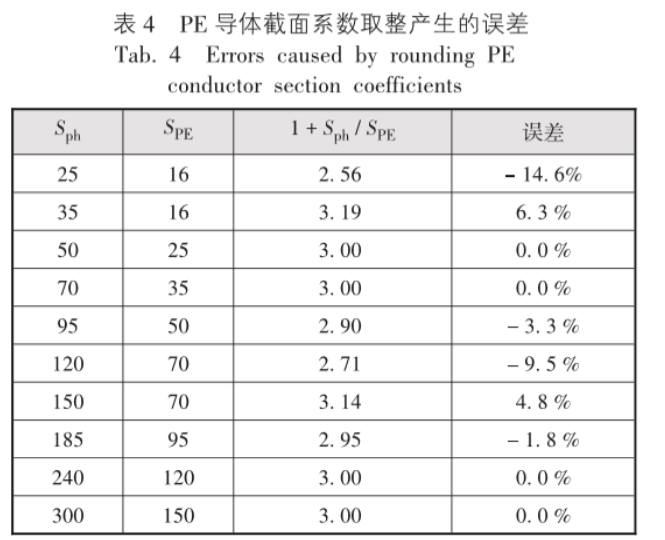
对查表来说,表格数字太多不方便使用。文献[1]为了使这个系数的修正表格简单而进行了取整;文献[2]则是做了一个比较复杂的表格;文献[3]表11.2 - 4直接将常用的电缆做进表格,使用起来会更方便一些。
电缆电抗校正系数
电缆电抗校正系数出现的原因主要是因为通用法的简化计算公式中只反映了电阻,没有反映电抗,从数值上看,就是电阻和阻抗的比值。对于同一截面的导体,电抗值和导体排布有关,电阻值和导体温度有关。下面取文献[3]中电缆参数进行复核,如表5~表7所示。
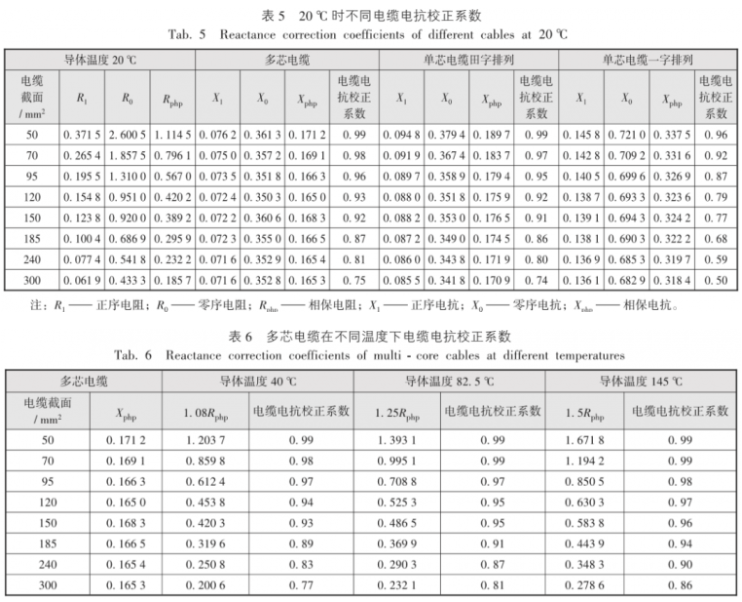
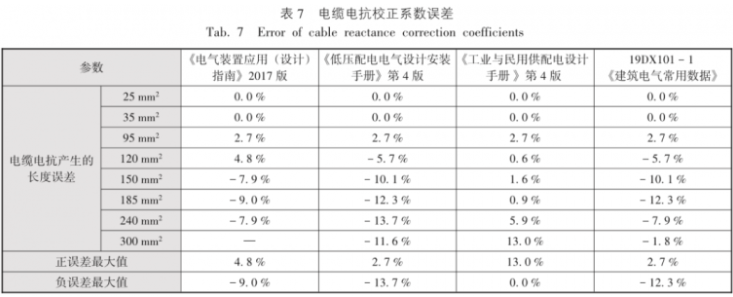
从表5数据对比可以看出,多芯电缆和单芯电缆田字排列的数据非常接近,几本资料的电缆电抗校正系数基本是按多芯电缆或单芯电缆田字排列而不是单芯电缆一字排列进行取值的。另外导体温度越高,电阻值越高,电缆电抗校正系数也应该越高(如表6所示)。文献 [2] 的电抗校正系数取值接近20 ℃,导体电阻率的温度系数为1.5,按文献 [2] 的取值更容易通过GB 50303 - 2015的验收。以文献 [4] 的电阻率取值为参考值,文献 [1]~文献[4] 的电缆电抗校正系数都出现了较大的误差,如表7所示。
并联导体校正系数
文献 [2]~文献[4] 并联导体校正系数都采用了4(N - 1)/ N,(N2),这个系数最早应来自文献 [2],文献 [1] 中虽然没有明确并联导体校正系数,但在图表G36注(2)中提到如果每相中有多根并联导线,那么用总电阻除以导线的数量,电抗值实际上保持不变,在G47页的算例中C3回路的阻抗计算也体现了这点。
表8是电抗不变算法和4(N - 1)/ N算法的并联导体校正系数的比较。对于4(N - 1)/ N算法,当N无穷大时,电阻为0,剩下的只有电抗,此时电抗刚好是原阻抗的1 / 4是该算法成立的前提。如电抗与电阻的比值满足一定假设值,从N = 5开始电抗不变算法和4(N - 1)/ N算法的并联导体校正系数基本一致。
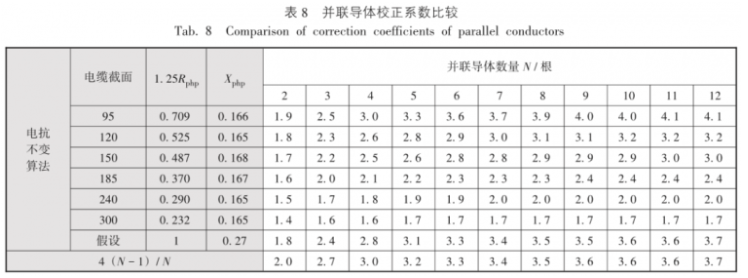
常规的电路并联阻抗计算,并没有电阻变、电抗不变的说法。但电抗值和导体排布有关,从表8看,95 mm2截面电缆的电抗和300 mm2截面电缆的电抗是基本一致的,如果采用4根195 mm2截面电缆成束代替1根1300 mm2电缆这种方式,这时回路电抗基本是不变的。所以,电抗不变算法更适用于每相电缆成束的情况,而不适用于常用的多芯电缆并列的情况,而文献[1]每相中有多根并联导线更准确的理解是每相多根电缆成束。
在DOCWIN中,有一个并联电缆对称安装的选项,同样10根电缆并联的回路,不打勾时并联电抗不变,打勾时并联电抗为原来的10 %。并联导体校正系数4(N - 1)/ N不建议采用,多芯电缆并列电抗应除以根数,多根单芯电缆成束电抗可不变。
灵敏度系数
灵敏度系数1.3始于GB 50054 - 1995《低压配电设计规范》(已废止)第4.2.3条,条文说明为按《低压断路器》(JB 1284 - 85)规定,保证断路器脱扣的电流为短路电流整定值的120 %,再考虑计算误差等因素。这个灵敏度系数1.3是专门针对某种断路器的,在其保证动作电流(120 % 短路整定电流)的基础上,增加了约10 %。由于间接接触防护电器的动作特性公式直接用了标准电压U0,并没有考虑最小短路电流的电压系数0.95,如折算为系数的话是1.2 / 0.95 = 1.26,而1.3和1.26的差别是考虑了其他误差等因素,其他误差系数大约是1.04。而对于瞬动上限已经是保证动作电流GB 10963.1的断路器,灵敏度系数考虑其他误差取1.1已经足够。
文献[3]中对电磁和电子式断路器采用不同的脱扣器系数指标,这个跟产品有一定关系,即使同类脱扣器也可能不一样,例如在文献[2]中表2.6 ~表2.8,ABB的T1、T2、T3断路器同样是 In = 100、I3 = 10 In的热磁脱扣器,对应35 mm2电缆的最大长度分别是42 m、50 m、58 m。
当回路首端电压明显低于95 % 标称电压时,电压系数应按实取值。
线路侧阻抗系数
文献[1]、[2]、[4]中线路侧阻抗系数都采用了0.8系数;文献[3]采用了0.8~1.0,当故障点远离配电变压器、线路截面积较小、变压器容量较大时,取高值(如0.95~1.00)。线路侧阻抗系数主要取决于电源侧阻抗和线路侧阻抗的比值,下面用这种思路试对该系数的选取进行分析。
以文献[3]表4.3 - 5中1 000 kVA变压器在100 MVA系统短路阻抗的数据为例,单相接地相保短路电流为22.73 kA,代表如忽略变压器至低压柜及低压柜内部母线的阻抗时,在出线断路器处产生22.73 kA的单相接地相保短路电流,将在断路器前端产生100 % 电压降。如果出线塑壳断路器短路整定值为3 kA,当单相接地刚好达到保证动作电流时,在断路器前端将产生31.2 / 22.73100 % =15.8 %的电压降,断路器后端的电压降为1 - 15.8 %= 84.2 %,这个数就是线路侧阻抗系数;如果出线塑壳断路器短路整定值为1 kA,则为1 - 11.2 / 22.73100 % = 94.7 %。这个结果也是偏保守的,因为断路器前端(靠近变压器端)的阻抗是偏电抗的,而断路器后端(刚好达到保证动作电流时远离变压器)的阻抗是偏电阻的,实际线路侧阻抗系数会比这个略大。
根据上面的分析,对于第一级配电线路的线路侧阻抗系数,可按下式估算:

其实式(5)的计算方法和组合法的想法是非常接近的。对于非第一级配电线路,如果可以获取断路器处的单相接地相保短路电流,也可以用同样的公式计算。当前段线路达到最大长度时,非第一级配电线路的线路侧阻抗系数也可以用类似的思路按下面的公式计算:
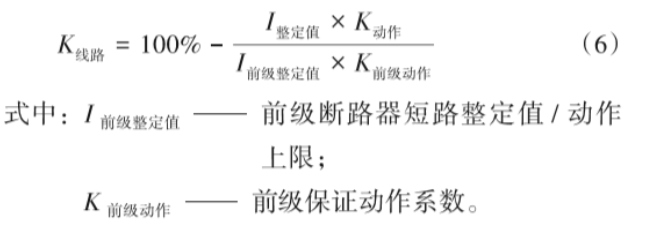
如前级采用出线塑壳断路器短路整定值为2 kA,线路达到最大长度,出线采用C20微断,线路侧阻抗系数 = 1 -(2010) / (2 0001.2) = 91.7 %。但当出线塑壳断路器整定值为1 kA时,线路侧阻抗系数 = 1 - (1 0001.2) / (2 0001.2) = 50 %。可见线路侧阻抗系数的取值是比较复杂的,即使同一个低压配电柜或配电箱处不同的出线断路器的差异也是非常大的,直接设定一个值并不合适,也不完全是故障点离变压器距离的问题。线路侧阻抗系数取0.8或者0.8~1.0的误差可能非常大。
综合误差分析
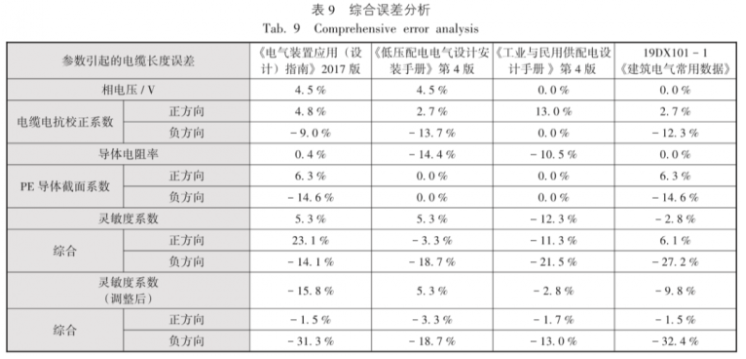
从前面的分析可知,并联导体校正系数、线路侧阻抗系数需要单独计算,目前几个常见简化计算公式都可能产生较大的误差,这里不将上面2个系数纳入误差分析。另外,由于验收规范有一定的不合理性,暂用BS 7671的温度系数、电压系数取值,灵敏度的标准采用了塑壳断路器保证动作电流 / 电压系数 = 1.2 / 0.95 = 1.263。
表9综合误差分析未考虑PE导体截面系数和电缆电抗校正系数在特定截面的误差部分抵消,从结果看:文献[2]和文献[3]均无正方向误差;文献[1]和文献[4]均有正方向误差。如不改变其他取值的情况下,将灵敏度系数分别调整为1.5、1.2、1.3、1.4,则4种方法的综合误差均无正方向误差,从安全角度考虑是可用的。但如果一定要达到GB 50303 - 2015的要求,上述灵敏度系数还需进一步加大。灵敏度系数和计算方法、参数取值、计算目标相关,单独谈灵敏度系数没有意义,在IEC和BS标准中也并没有灵敏度1.3的说法。
接地故障保护校验的建议
简化计算公式和相应表格的目的是减轻工作量,但肯定会产生一些误差,在应用时要知道误差的范围。如果表格最大允许长度的误差是0~- 30 %,查表结果是100 m,当实际长度100 m时是满足的,实际长度 > 142 m时是不满足的,而100 m < 实际长度142 m是否满足需要用更准确的方法复核。误差范围越小,需要复核的可能性就越低,复核工作量就越少。从表9可以看出,文献[3]只要将电缆电抗校正系数优化,综合误差就基本没有了。
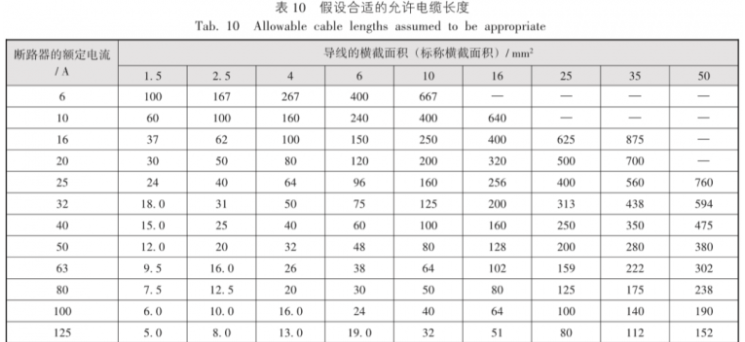
这里提供一个通过合适的允许电缆最大长度表格判断末端线路接地故障环路阻抗是否满足瞬动要求的思路,假设从低压柜出来第一段线路516 mm2 80 m,第二段线路56 mm2 60 m,末端线路32.5 mm2 80 m,判断末端采用C10A微断是否满足瞬动要求。
表10引自文献[1]图表G49,该表格线路侧阻抗系数为0.8。暂假设所有参数的取值除线路侧阻抗系数外均是合适的,那么线路侧阻抗系数为1时所有长度要乘以1.25。第一段在C10微断保证动作电流下接地故障压降是 80 /(640 1.25)= 10 %;第二段是 60 / (2401.25)= 20 %,考虑这个电流在低压柜前基本不产生压降,那末端线路接地故障压降是100 % - 10 % - 20 % = 70 %,末端线路最大允许长度是70 %(1001.25) = 87 m,80 m小于87 m满足瞬动要求。当有一个参数取值合适的表格时是可以较准确地判断接地故障环路阻抗是否满足瞬动要求,不需假设一个线路侧阻抗系数。
采用仪表测量接地故障环路阻抗也会有误差,如某数字仪表测试接地环路阻抗精度为:0.01 ~9.99 ( 5 %0.03 )时,其相对误差见表11。
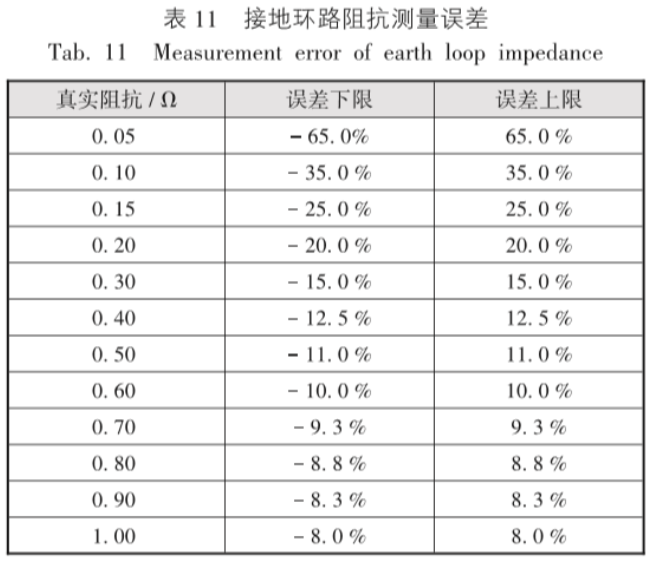
当真实阻抗小于0.2 时,测量误差已经比较大了,这时保证动作电流约为1 100 A,比I3 = 10 In的100 A塑壳断路器的要小。目前能够直接测量得到相对误差较小的也仅仅是保证动作电流较低末端的回路,IEC标准中仅对32 A以下的末端回路要求0.4 s内动作也是有一定原因的。
总结
目前,现有的TN - S系统接地故障保护最大允许电缆长度计算方法和表格在应用和误差方面都存在或多或少的问题,设计人员在使用时需要注意判断。
GB 50054 - 2011对TN - S系统配电线路或仅供给固定式电气设备用电的末端线路的间接接触防护电器切断故障回路的时间不宜大于5 s,所以对一般配电线路来说,要求电缆小于最大允许长度是没有必要的。但采用单磁断路器做配电线路保护的情况,电缆实际长度大于最大允许长度不是0.4 s或5 s内能不能切断的问题,而是一直无法切断的问题。
发生接地故障时单磁断路器动作是必须要保证的,但保证动作电流较大时数字仪表测量接地环路阻抗的相对误差较大,而如何较准确计算没有明确的规定,在工程中容易留下较大隐患。灵敏度1.3与诸多因素有关,不建议无前提单独存在。GB 50303 - 2015的系数取值建议参考BS 7671 - 2018,可以进一步要求测试时的条件、允许按实际情况适当调整系数、明确允许一些可行的精确评估方法。此外,应防止人为避开易出现问题回路的抽查,对单磁断路器配电回路建议全面或重点检查。