1、剥离及采煤施工土石方计量的特点(1)工程量大。剥离及采煤工程量大,精确计量困难,计量结果与经济利益直接挂钩,计量及结算过程中争议大;
(2)单价不同。由于岩石剥离需要爆破,剥离难度比表土要大,二者发包单价可能不一样,计量时需对二者区分;
(3)分别计量。对不同性质、硬度的岩石可能制定不同的单价,计量时要求将不同性质、类别的岩石/表土区分开,分别计量;
(4)连续计量。剥离及采煤施工有一定连续性,需要多次中间计量,计量时需要从已经施工的工作界面处进行。选择剥离及采煤工程量计量方法时,要求计量方法相对简单易懂、容易操作、容易核对、误差较小且能适应连续计量的需要。由于剥离及采煤工程量计量存在上述问题,如何选取计量的方法就显得至关重要。
2、不同的剥离体积计算方法
2.1方格网法方格网法就是用固定尺寸的方格网对挖方范围进行有规则的分块,先计算出每一个小方格块的体积,体积之和就是整个挖方体积。选取的方格网大小决定了最终的计算精度。剥离工程土石方工程量一般较大,考虑边坡与不考虑边坡时的体积之差绝对值相对较大。用方格网法计算时,对于挖方的边坡问题,有不同的处理方法,分述如下:
2.1.1不处理边坡的情况一般挖方的结果都是挖出一个顶面积大底面积小的坑状结构,设S1为挖方顶面面积,S2为挖方底面面积,则一般情况下S1>S2。计算土方量时,可以S1的边界为计算范围向下做垂直切割,以原始地面标高数据为顶面,以测量的底面坐标高程数据所织成的三角网为底,计算出体积V顶。同样以底面面积S2的边界为计算范围向上做垂直切割,以原始地面标高数据为顶面,以测量的底面坐标高程数据所织成的三角网为底,计算出体积V底。上述两个体积可以用软件很方便的进行计算。实际挖方体积v可以认为是:V=(V顶+V底)*0.52.1.2用三角网织出边坡的情况既然是利用方格网法计算挖方工程量,在方格网的顶面标高确定的情况下,方格网的底部标高高程数据就决定了每一个方格网的体积。在织底部三角网时,可以考虑将边坡处的坐标高程及边坡坡顶处的坐标高程一并作在一起,相当于将底及四周认为是一个整体的盆状结构,原始地面标高为盆顶,盆底及盆顶所围成的结构体积就是要计算的挖方体积。
2.2断面法假设每隔一定距离(如20m)选一断面。断面法算量的基本原则就是将不规则结构体分割成相对比较规整、可以用数学方法近似计算的结构。同样切割出的断面也有不同的体积计算方法。
2.2.1以断面的切割面面积为上下底计算在这种情况下,断面之间的垂直距离h是可以确定的,只要确定出切割形成断面的具体面积S1和S2,则可以用:V=(S1+ S2)*0.5*h来确定两个断面之间的结构体积,所有断面所形成的结构体积之和就可以认为是整个挖方结构的体积。
2.2.2以切割形成结构的上下面为顶底面计算以切割形成结构的上下面为顶底面计算体积时,以顶面面积S1和底面面积S2及顶底面之间的距离h为依据据来计算体积。确定S1时可以该面的水平投影面积代替,S2可以用同样的方法处理,以底面的水平投影面积代替。h的确定就比较复杂了,可分别求出顶面和底面测量数据标高的平均值,h值可以该平均值之差来近似代替。这种方法要求测量的高程点均匀、有规律,取舍高程点时的人为倾向对结果可能造成一定影响。在土方挖掘量比较大时,若每一切割结构体的h都同时偏大或偏小,对最终结果造成的影响将是很可观的。
2.3直接切割算量
2.3.1 手工直接在图纸上切割算量这种情况和断面法计算有点类似。可以凭借观察将结构划分成比较规则的可以用数学方法直接计算的形状,用比例尺在图纸上量出长度及距离,通过观察得到相应的高程差,计算出单个结构的体积,体积相加就为总体体积。这种方法简便易懂,不需要计算机及专业计算软件等工具。可以用于工程量的大致估算,计算过程不复杂,计算结果在估算的程度上可以采用。缺点是精度比较低,误差较大且无法纠正。在计算条件不具备且对结果要求不太高的地方可以采用。
2.3.2 在计算机上切割算量这种方法与上述方法类似,只不过具体的切割过程避免了手工做图操作上的误差,但依然需要采用人为方式来确定挖方体结构的高度,依然不能有效处理边坡对体积的影响。
3 三种剥离体积计算方法的比较
(1)方法一中计算每个方格网的体积及体积相加完全可以通过软件来完成(如南方CASS等),这种方法充分利用了计算机的数据处理功能。在数据确定的情况下计算结果唯一,比较容易核对和检查,方便直观。在边坡角不一致时,可以顶面、底面面积为范围垂直切割所形成的结构体积的平均为所求挖方的体积,这种情况有一定误差,但计算过程简便,可以在很短时间内确定出具体的体积。若将整个边坡(包括坡顶、坡底)与底面一起织成三角网作为计算体的底面来计算体积,在边坡比较平缓的情况下,方格网取的越小则计算精度越高;在边坡较陡的情况下很明显误差将会加大,且计算结果是比真实体积要少。一般剥离测量时,原始地面及开挖后的底面标高以数据形式测得。总体说来,这种方法的计算精度相对较高,且快速、合理、直观,适用范围广泛。
(2)方法二断面法计算时,工作量相比方格网法有所增大,尤其是确定每个断面(顶面、底面)面积时,即使用软件计算确定断面面积也比较麻烦,且容易出现差错。这种方法优点是比较直观易懂,但计算过程较复杂,不容易核对,断面的切割方法不确定,随着工程向前推进,断面的切割方法及切割位置也需要变化,不适于操作。在结构比较均匀变化不大时,用这种方法计算比较合理,一旦结构变化较大用断面法处理时就会产生较大误差。以切割形成结构的上下面为顶底面计算时,面及面之间的距离都是确定的,体积比较容易确定;以正常切割断面所形成的上下面为顶底面计算体积时,顶面与底面之间的距离要靠观察数据来确定,操作者站在不同的立场,取点时会有不同倾向,实际应用中,这种方法的操作会受到一定影响。
(3)方法三手工切割算量,误差较大。即使在计算机上精确测量距离和高度同样会产生较大误差。这种方法切割断面时人为的主观因素较大,不同人、不同的切割方法都会产生不同的计算结果,可核对及可对比性差;精度比较低,误差较大且无法纠正。在计算条件不具备且对结果要求不太高的地方可以采用。
4 一个例子:图1为为新疆哈密地区巴里坤县别斯库都克露天煤矿工程2008年12月开工至2009年1月中旬的土方开挖图,地表标高已全部采集,图1周围边线分别为开挖后的坡顶边界线和坡底边界线,坡顶与坡底的连线就形成了边坡,边坡角不固定。开挖结果为坑底宽25-80米、长1.28km的开挖沟。原始地面标高数据、挖方后的沟底及坡底坐标高程数据都已测得。

图1 工程开挖图(坡顶、坡底连线)4.1 方格网法计算体积4.1.1不处理边坡直接用坡顶、坡底线为范围垂直切割所圈成的结构计算体积。坡底坐标高程点所织成的三角网如图2:


图2 坡底坐标高程点所织成的三角网图3 包含了边坡的沟底三角网
4.1.2用三角网织出边坡将边坡的坡底高程坐标数据从原始地表高程中读出,与坡底三角网一起织成一个网,该网包含了开挖沟底及边坡的相关数据(见图3)。4.2 断面法计算体积可以设计以20m为间距做切割断面,如图4。
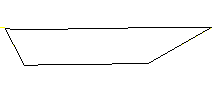
图4 每隔20米切割断面图4.2.1以切割的断面面积为上下底计算其中两个断面切割所形成的图形如下(图5),可以很方便利用CAD计算出该断面面积。依次计算出所有断面的面积,可以得到两个断面之间结构的体积,体积之和即为总挖方体积。
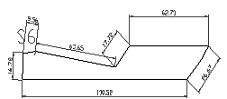
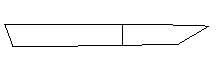
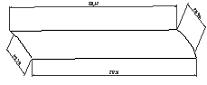
图5 其中两个断面形状图6切割的其中一个图形
4.2.2以正常上下面为顶底面计算方法与上4.2.1相同。唯一区别是不以切割面为顶底,而以正常上下面为顶底面计算。4.3手工法计算用手工直接在图纸上切割与用计算机直接切割的原理是一样的,只是精度不同。切割的其中一个图形见图6。该图形就可以大概认为是个规则的矩形,可以利用比例尺量出矩形的长和宽,进而计算出面积,观察顶、底面的高程点,读出一个基本合适的高程数据,进而计算出体积。
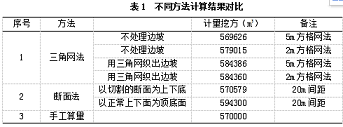
图6 用手工法切割的一个图形4.4 不同方法计算结果计算结果对比情况见表1。

5、结论(1)误差。不同的计算方法结果不可能完全一样,会有一定的误差,一定情况下,误差相对较大,见表2。与该误差相对应的经济利益是很可观的。选取不同的体积计算方法对结果会有影响。在剥离体积较大时,误差的绝对值也相对较大,相对应的经济利益非常可观。
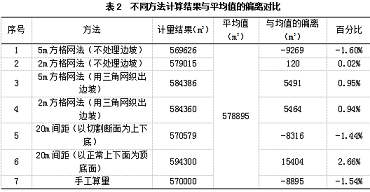
(2)方格网的选取对结果的影响。方格网选择的越小则计量相对越精确。这种情况下,可以充分发挥计算机算量的优越性。能在相对较短的时间内给出较精确的结果。且实践证明,当选取的方格网达到比1m还小时方格网的大小对计算结果与的影响基本可以忽略。(3)边坡。若剥离是连续进行的,则边坡的问题可以不予考虑。因为边坡也是移动的,随着剥离的进行,边坡的位置甚至坡度都将发生变化。除非精确计量,否则非固定帮的边坡可以不予考虑。(4)连续计量。方格网法适合于一次性计量,能相对较精确。但若考虑到连续施工及多次计量的情况,方格网法由于需要单独织出不同的顶和底面,不易操作;此时断面法的优点比较突出,断面线固定,做出的断面同时也是固定的,连续施工时只需在已经做好的断面基础上继续做即可。(5)分类计量。分成若干类计量时,若采用方格网法则需织出不同的顶、底面,分的类别越多,编织的工作量越大,精度越低。断面法不存在这种问题,若选取切割的断面为上下底计算的话,可以很方便地在断面上区分不同类别的剥离物,且可以方便的计量。经过多次尝试及比较,别斯库都克露天煤矿的土石方剥离及采煤计量工作采用断面法(以切割面为顶底面)进行计算,取得了较好的效果,有效避免了验收及计量争议。
