今天,我们就来分享一下如何利用反弯点法快速得到框架结构的内力。何为反弯点法?框架结构在水平荷载作用下的弯矩图如下图所示,仔细观察一下柱子的弯矩图,在柱子中间有一个位置,弯矩为0,这个点称之为反弯点。我们知道,在水平荷载作用下,每根柱子中的剪力在柱子的高度范围内是保持不变的(如果这一点无法理解,请在微信平台内回复材力目录,查看梁的弯矩图和剪力图相关内容)。由于剪力在整个柱子范围内的数值是一样的,因此,只要我们确定了反弯点的位置,就可以用剪力来乘以反弯点与柱子两个端点之间的距离来,来确定柱端弯矩。那么,反弯点的位置到底在哪呢?反弯点法假定对于底层柱子,反弯点的位置在距基础2/3柱高处,对于其他层,反弯点均位于柱高的中点,如下图所示。
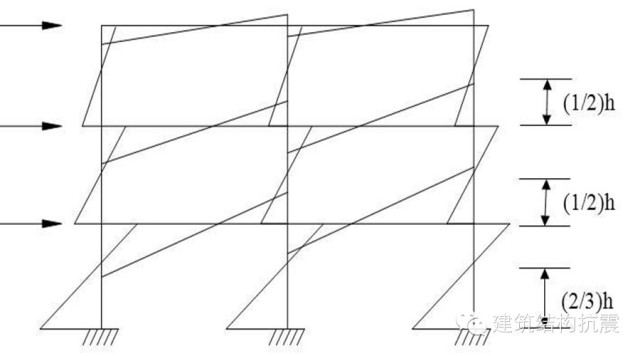
由每层的地震作用,可以得到每一层的水平剪力,根据柱子的刚度大小,将每一层的剪力分配到该层所有柱子上。(想知道水平剪力为何在柱子间按刚度进行分配,请在微信平台内回复短柱查看详细内容)。对于梁,我们关心的内力是梁的剪力和弯矩,对于柱子,除了剪力和弯矩,我们还关心柱子的轴力。这么多的内力,究竟应该从哪入手才能把所有的内力快速求解出来?求解框架结构内力的流程图如下:

以一个二层两跨框架结构为例,讲解一下求解框架结构内力的流程。
(1)柱端弯矩的确定
由前面叙述可知,对于柱子,可以根据反弯点的高度和柱子的剪力,得到柱端弯矩,如下图。
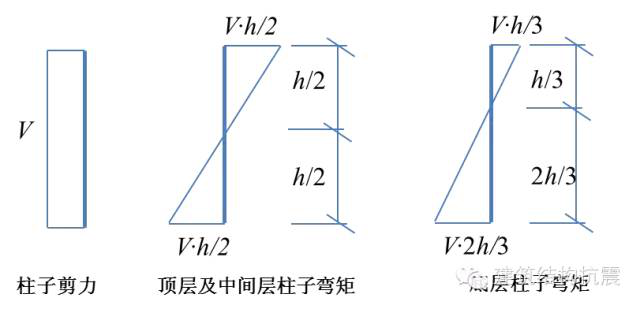
总的框架柱弯矩图如下:
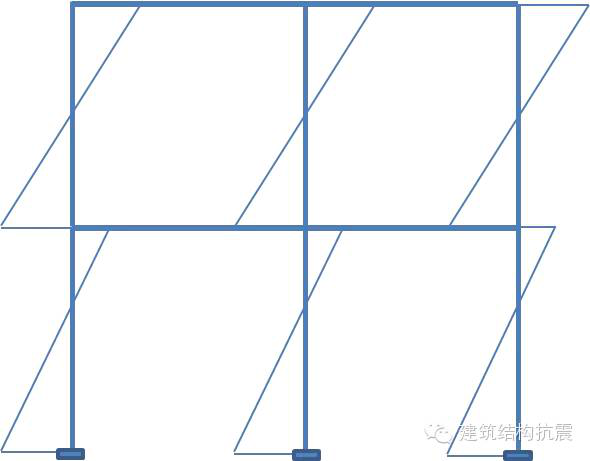
(2)梁端弯矩的确定
梁端弯矩需根据柱端弯矩按照节点平衡条件确定。对于边柱节点,梁端弯矩等于柱端弯矩之和,如下图所示,上柱端弯矩为

,下柱端弯矩为
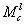
,因此梁端弯矩为
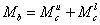
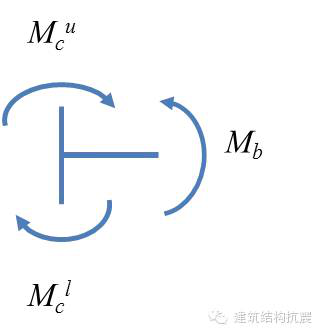
而对于中间节点,由于不止一根梁相交于此,梁端弯矩之和等于柱端弯矩之和,而每个梁端弯矩,要根据梁的线刚度进行分配。线刚度的定义为梁的抗弯刚度(EI)除以梁的跨度L,即(EI/L)。如下图所示梁柱节点,左梁的弯矩为
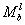
,右梁的弯矩为

,则梁端弯矩和应为,
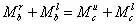
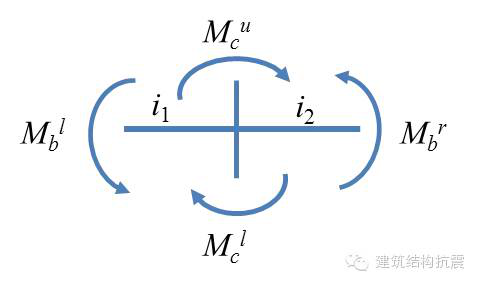
如果左梁和右梁线刚度分别为i1和i2,则梁端弯矩应为
最终可以得出框架结构弯矩图为

(3)梁端剪力。
梁端剪力需要由梁端弯矩,按照平衡条件确定。如下图所示,已知梁端弯矩M1和M2,梁的跨度为 L ,则梁端剪力应为V=(M1+M2)/l。

(4)柱子轴力的确定。
水平荷载作用下产生的柱子轴力,需由梁端剪力来计算。如下图所示,根据梁柱节点的受力示意图,梁端剪力与其作用在柱子上的轴力大小相等,方向相反。
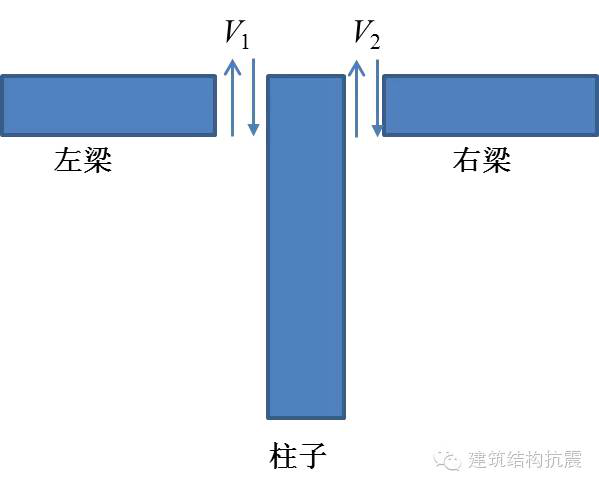
如果顶层中柱左梁剪力V1 ,右梁剪力V2,由于柱子轴力通常取受压为正,因此柱子的轴力由梁端剪力计算为V1-V2。需要注意的是,除顶层柱外,下层各柱的轴力计算时,需要叠加上部各层柱子的轴力,最终的轴力图形式为

至此,框架结构全部内力都已经求得。