1. 计算原理
平面弹性地基梁法假定挡土结构为平面应变问题,取单位宽度的挡土墙作为竖向放置的弹性地基梁,支撑和锚杆简化为弹簧支座,基坑内开挖面以下土体采用弹簧模拟,挡土结构外侧作用已知的水压力和土压力。图 6-5 为平面弹性地基梁法典型的计算简图。
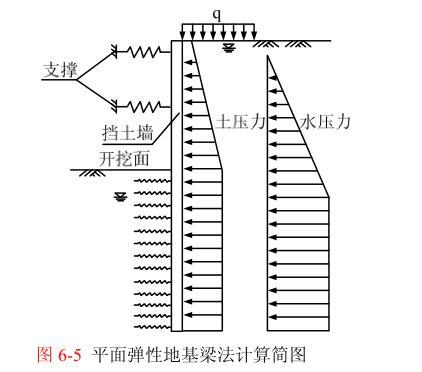
取长度为 b0 的围护结构作为分析对象,列出弹性地基梁的变形微分方程如下:

考虑土体的分层(m 值不同)及水平支撑的存在等实际情况,需沿着竖向将弹性地基梁划分成若干单元,立出每个单元的上述微分方程,一般可采用杆系有限元方法求解。划分单元时,尽考虑土层的分布、地下水位、支撑的位置、基坑的开挖深度等因素。分析多道支撑分层开挖时,根据基坑开挖、支撑情况划分施工工况,按照工况的顺序进行支护结构的变形和内力计算,计算中需考虑各工况下边界条件、荷载形式等的变化,并取上一工况计算的围护结构位移作为下一工况的初始值。
弹性支座的反力可由下式计算:

2. 支撑刚度计算
对于采用十字交叉对撑钢筋混凝土支撑或钢支撑(如图 6-6 所示),内支撑刚度的取值如下式所示:


对于复杂杆系结构的水平支撑系统,不能简单地采用式(6-3)来确定支撑的刚度,但较合理地确定其支撑刚度也很困难。国家规范建筑基坑工程技术规范 [2] 建议采用考虑围护结构、水平支撑体空间作用的协同分析方法确定。
当采用主体结构的梁板作为水平支撑时,水平支撑的刚度可采用下式来确定:

3. 水平弹簧支座刚度计算
基坑开挖面或地面以下,水平弹簧支座的压缩弹簧刚度KH可按下式计算
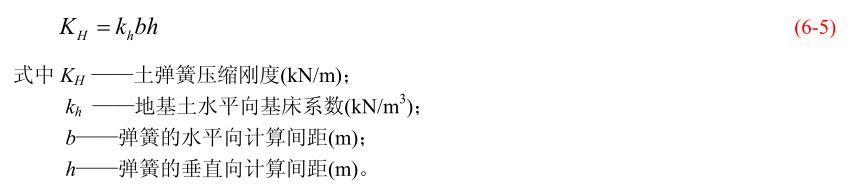

图 6-7 给出了地基水平基床系数的五种不同分布形式,地基水平向基床系数采用下式表示:

当有土的标准贯入击数 N 值时可用经验公式求水平向基床系数:

若假设水平向基床系数沿深度为常数或在一定深度其值达到不变值时可按表 6-1 中的经验值取值。

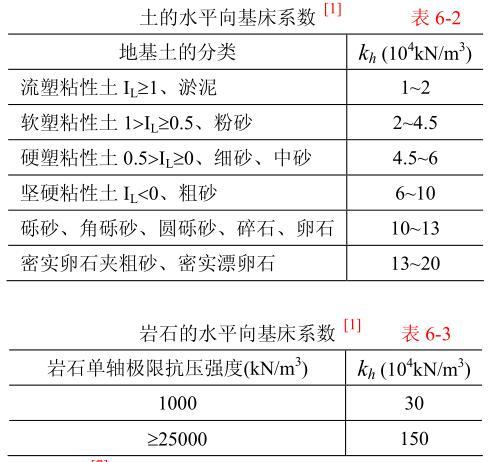
中国《公路桥涵设计规范》(1975 年试行本)和胡礼人著《桥梁桩基设计》分别给出了各类土和岩石的水平向基床系数经验参考值,如表 6-2 和表 6-3 所示
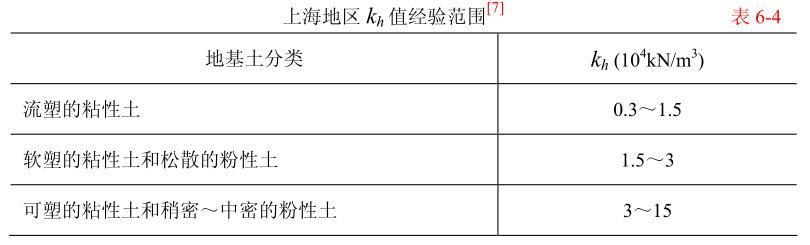
上海市基坑工程设计规程根据上海地区的工程经验,对各类土建议了如表 6-4 所示的水平向基床系数值范围。

根据公式(6-6)中指数 的取值不同,将采用图 6-7 中(a)、(b)、(d)的地基反力分布形式的计算方法分别称为张氏法、C 法和 K 法。图 6-7 (c)中,取 n=1,A 0 =0 则

此式表明地基水平向基床系数随深度按线性规律增大,由于我国以往应用这种分布模式时,采用 m 表示比例系数,即 k h =mz,故通称 m 法。
基坑围护结构的平面竖向弹性地基梁法实质上是从水平向受荷桩的计算方法演变而来的,因此严格地讲地基土水平抗力比例系数 m 的确定应根据单桩的水平荷载实验结果由下式来确定:

在没有单桩水平荷载实验时,建筑基坑支护技术规程提供了如下的经验计算方法:

公式(6-10)是通过开挖面处桩的水平位移值与土层参数来确定 m 值,公式中的取值难以确定,计算得到的 m 值可能与地区的经验取值范围相差较大。而且当k 较大时,计算出的 m 值偏大,可能导致计算得到的被动侧土压力大于被动土压力。
杨光华指出采用公式(6-10)计算广州地区的岩石地层的 m 值将明显偏低。湖北省地方标准基坑工程技术规程 [6] 在上式前乘了一个经验系数,对一般粘性土和砂土经验系数取1.0,对老粘性土、中密以上砾卵石取 1.8~2.0,而对淤泥和淤泥质土则取 0.6~0.8。建筑桩基技术规范 [3] 根据试桩结果的有关统计分析亦给出了各种土体 m 值的经验值,如表 6-5 所示。
但这里的 m 值与水平位移的大小相关,当围护结构的水平位移与表中对应的水平位移不符时,需对 m 值作调整。

上海市基坑工程设计规程根据上海地区的工程经验,对各类土建议了如表 6-6 所示的m 值范围,可以作为软土地区 m 值的参考。

冯俊福根据杭州地区二十多个基坑 m 值的反分析,并结合该地区的工程经验,建议了杭州地区的 m 值范围,如表 6-7 所示。

从上述有关 m 值的确定方法可以看出,不同的规范或规程得到的 m 值的范围可能相差较大,因此 m 值的确定在很大程度上仍依赖于当地的工程经验。
4. 主动侧土压力的计算
5. 求解方法
基于有限元的平面弹性地基梁法的一般分析过程如下:
(1) 结构理想化,即把挡土结构的各个组成部分根据其结构受力特点理想化为杆系单元,如两端嵌固的梁单元、弹性地基梁单元、弹性支撑梁单元等。
(2) 结构离散化,把挡土结构沿竖向划分为若干个单元,一般每隔 1~2m 划分一个单元。为计算简便,尽可能将节点布置在挡土结构的截面、荷载突变处,弹性地基基床系数变化处及支撑或锚杆的作用点处。
(3) 挡土结构的节点应满足变形协调条件,即结构节点的位移和联结在同一节点处的每个单元的位移是互相协调的,并取节点的位移为未知量。
(4) 单元所受荷载和单元节点位移之间的关系,以单元的刚度矩阵[K] e 来确定,即

作用于结构节点上的荷载和结构节点位移之间的关系以及结构的总体刚度矩阵是由各个单元的刚度矩阵,经矩阵变换得到。
(5) 根据静力平衡条件,作用在结构节点上的外荷载必须与单元内荷载平衡,单元内荷载是由未知节点位移和单元刚度矩阵求得。外荷载给定,可以求得未知的节点位移,进而求得单元内力。对于弹性地基梁的地基反力,可由结构位移乘以基床系数求得。
