1、引言
随着我国城市化的推进及满足国民对公共交通的需求,很多城市都在建设地铁,地铁车站大都采用明挖法施工,地下连续墙是众多支护中应用最广泛的基坑维护结构。从1863年世界最早的伦敦地铁开通以来,地铁已经在近100个城市运行,目前,北京、上海地铁通车运营里程已达500公里以上,同时我们有20多个城市正在或者申请修建地下铁道解决城市交通问题,我国目前处在地铁工程开发的高潮,因而对这类工程的地下结构施工提出了更高的要求。

地下连续墙钢筋笼的传统设计通常不考虑其在吊装施工过程中的受力[1]、[2]。施工分析采用附加加固钢筋组成的纵向、横向钢筋桁架作为支撑结构保证钢筋笼吊装过程中的整体刚度和几何稳定性。但是,这种方法缺乏理论计算,容易造成事故或者材料浪费。鉴如此,赵兴波等[3]进行了地下连续墙钢筋笼吊装方案研究,分析了钢笼刚度和吊点位置;杨宝珠等[4]利用Abaqus软件对钢筋笼吊装过程进行模拟,为相关工程提供了参考依据。同济大学朱大宇[5]对整个GFRP筋笼吊装过程进行了有限元建模分析。Xin Wang等[6]应用Ansys对大跨度钢结构吊装吊点进行了优化分析;S Rajasekaran[7]对海洋平台吊装进行了吊点位置优化分析。
传统有限元方法模拟吊装需要应用刚体方法获得不同位置时每根绳索的力,再把这些力施加到钢筋笼上,对钢筋笼每个独立位置进行有限元分析。本文应用有限元分析软件Abaqus[8]对钢筋笼进行数值模拟,利用Abaqus的Slip Ring单元对滑轮的运动进行模拟,避免了传统方法由于钢筋笼自身变形带来的误差,特别是对于像GFRP筋笼此类大变形结构如果采用传统方法会有很大误差。另外本文还应用多学科多目标优化软件Isight[9]对地下连续墙钢筋笼吊点位置进行优化。
2、钢筋笼有限元模型
2.1有限元模型
本文以图1所示某地下连续墙钢筋笼吊装为工程背景,该地下连续墙钢筋笼长45.8米,宽6米,厚0.86米。

图1 钢筋笼吊装示意图
分析采用Abaqus三维有限元分析软件,地下连续墙钢筋笼有限元模型所有单元模型采用B31梁单元和S3R壳单元模拟,吊装结构还包含8条绳索和8个滑轮,绳索应用只抗拉,不抗压和弯的索单元模拟,而滑轮利用Abaqus的SlipRing连接单元模拟,该单元很好模拟滑轮的力学特性。

2.2Slip Ring单元描述

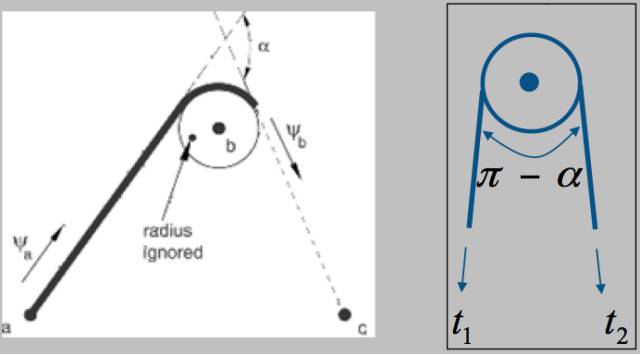
图2 Slip Ring滑轮连接单元
3、工况及结果
分别计算地下连续墙钢筋笼两种工况:重力作用和主吊提升10m。
3.1重力作用
约束滑轮1、2、5、6中心点,施加重力加速度,达到平衡后绳索的变形情况如图3所示,钢筋笼的垂直变形5.6cm。
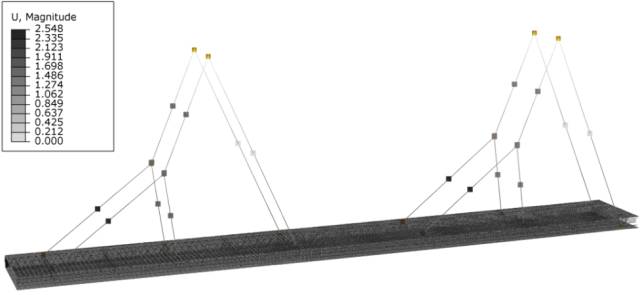
图3 平衡后绳索的变形
各绳索的荷载分担比如表1所示,索8的荷载分担比最大,达到19%。
表1 绳索的荷载分担比

沿长度方向的弯矩图如图4所示,图4横轴表示钢筋笼归一化长度,在总长68%的位置弯矩最大,达570KN/m

图4 沿长度方向的弯矩图
3.2主吊提升10m
次吊位置不变,即滑轮1、2固定,主吊滑轮5、6提升10m,绳索的变形情况如图5所示。
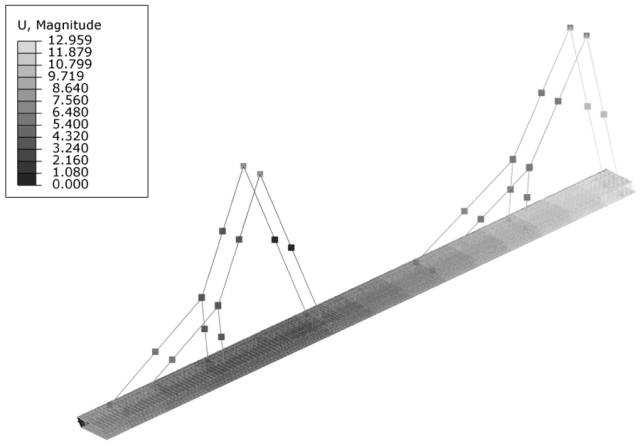
图5主吊提升10m后绳索的变形
提升过程中各索的拉力随主吊提升高度的变化如图6所示,横轴表示主吊提升高度。
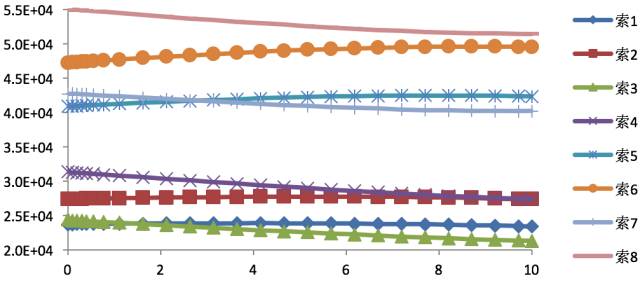
图6 索的拉力变化
4、钢筋笼吊点位置优化
钢筋笼采用整体起吊,由于其整体刚度较差,起吊时容易造成绕度过大、甚至整幅钢筋笼破坏的事故,所以起吊点的位置确定对起吊非常重要,本文采用参数化优化软件Isight对吊点位置进行优化。
由于需要参数化吊点的位置,上述模型太复杂,无法参数化,需要对模型进行简化,本文根据质量等效和刚度等效,简化为壳单元,简化模型如图7所示。优化工况仅考虑重力作用,在重力作用下利用简化模型获得的钢筋笼最大垂直变形是4.9cm,和非简化模型计算的5.6cm基本接近。

图7 简化壳模型
优化参数仅考虑横向加强板的位置优化,优化的参数如图7所示共5个吊点位置,吊点的设计变量区间如表2所示。
表2 吊点的设计变量区间

优化目标为最小化起吊时的钢筋笼绕度即最大垂直相对变形,可以通过Python语言读取Abaqus的odb文件获取钢筋笼局部坐标系下垂直位移的相对最大值和最小值获得,其差就是最大垂直相对变形。优化分析还需要实现流程自动化,本文应用Abaqus/CAE录制分析流程,生成rpy脚本文件,需要注意的是对于吊点位置要参数化,以便Isight驱动rpy文件改变吊点位置,同时为降低计算量,优化变量的变化并不是连续的,而是按照0.5m的倍数变化。
优化经过40多次迭代,优化后绕度降低了14.7%。
5、结论
本文应用Abaqus软件对地下连续墙钢筋笼吊装过程进行受力分析,并结合Isight软件优化吊点位置。
(1)和传统的应用刚体力学方法计算绳索的拉力,然后把获得的绳索的拉力施加在地下连续墙钢筋笼结构上分析钢筋笼的受力情况不同,本文直接用Abaqus的滑轮单元,自动平衡重力,获得平衡点的绳索拉力和钢筋笼的应力变形情况,可以更精确分析大变形问题,同时也可以实现吊装过程、而不是几种吊装状态的模拟,自动平衡重力的实现也为优化的实现提供了条件。
(2)应用简化模型和Isight软件自动对地下连续墙钢筋笼吊点位置优化,大大提高了优化效率,为吊装提供了安全保障。
(3)更进一步还可以对吊机的运动轨迹进行优化。
参考文献:
[1]李少利. 超深地下连续墙钢筋笼制作与吊装技术[J] . 隧道建设, 2011, 31(6):717-721.
[2]张宏斌. 地下连续墙施工中钢筋笼吊装技术钟伟 [J]. 隧道建设, 2010(s1):446-450.
[3]赵兴波, 茅利华, 龚振斌, 等. 上海M8线淮海路地铁车站43.0m 超深地下连续墙钢筋笼吊装[J]. 建筑施工, 2004(1): 10-11.
[4]杨宝珠, 邵强, 丁克胜, 等. 超深、超大地下连续墙钢筋笼吊装过程研究[J]. 工业建筑, 2013(7): 101-104.
[5]朱大宇. GFRP筋地下连续墙的施工应用研究[D].上海: 同济大学, 2008.
[6]XWang, X Lei, X Cao, Y Zhou,S Gao. Optimization of Lifting Points of Large-Span Steel StructureBased on Evolutionary Programming[J]. Springer Berlin Heidelberg, 2012,7473:315-322.
[7] SRajasekaran, S Annet, Y Sang Choo., Optimal Locations for Heavy Lifts forOffshore Platforms. Asian Journal of Civil Engineering (Building and Housing), 2008,9(6), 605627.
[8]Abaqus 2017x Help Documention[M]. USA: DASSAULTSYSTEMES Simulia Corp., 2017.
